קומבינטוריקה

קומבינטוריקה היא אמנות הספירה. היא עוסקת בבחירות, סידורים וצירופים של אובייקטים. שאלות כוללות קביעת מספר הדרכים לביצוע משימות, סידור פריטים (תמורות), או בחירת תת-קבוצות (צירופים), תוך שימוש לעיתים קרובות בעקרונות כמו עקרון המכפלה ועקרון הסכום.

עקרון שובך היונים ספירה כפולה מקדמים בינומיים ומשולש פסקל כלל המכפלה תורת הגרפים התאמות אינדוקציה תורת המשחקים גאומטריה קומבינטורית אינווריאנטים בדיקת מקרים תהליכים טבלאות מספריות צביעות

  • חציית הנחל

    במהלך טיול כפרי מצאו עצמם מר וגברת סופטלי בדילמה נחמדה. הם היו צריכים לחצות נחל בסירה קטנה שיכולה לשאת רק `150` ליברות משקל. אבל מר סופטלי ואשתו שקלו בדיוק `150` ליברות כל אחד, וכל אחד מבניהם שקל `75` ליברות. ואז היה הכלב, שלא ניתן היה לשכנע אותו בשום אופן לשחות. על פי העיקרון של "נשים קודם", הם מיד שלחו את גברת סופטלי, אבל זו הייתה טעות מטופשת, כי היא הייתה צריכה לחזור שוב עם הסירה, כך שלא הושג דבר בפעולה הזו. איך הם הצליחו כולם להגיע לצד השני? הקורא יגלה שזה הרבה יותר קל ממשפחת סופטלי, כי האויב הכי גדול שלהם לא יכול היה לקרוא להם בצדק רביעייה מבריקה - בעוד שהכלב היה טיפש מושלם. מקורות:

  • חציית נהר אקס

    לפני שנים רבות, בימי המבריח הידוע כ"רוב רוי של המערב", כנופיית פיראטים קברה על חוף דרום דבון כמות של אוצר אשר, כמובן, ננטש על ידם בצורה בלתי מוסברת כרגיל. כעבור זמן מה, מקום הימצאו התגלה על ידי שלושה כפריים, אשר ביקרו במקום לילה אחד וחלקו את השלל ביניהם, ג'יילס לקח אוצר בשווי £`800`, ג'ספר בשווי £`500`, וטימותי בשווי £`300`. בחזרתם הם נאלצו לחצות את נהר אקס בנקודה שבה הם השאירו סירה קטנה בהיכון. כאן, עם זאת, הייתה קושי שלא ציפו לו. הסירה יכלה לשאת רק שני אנשים, או אדם אחד ושק, והיה להם כל כך מעט אמון זה בזה שאף אדם לא יכול היה להישאר לבד על היבשה או בסירה עם יותר מחלקו בשלל, אם כי שני אנשים (בהיותם בלמים זה על זה) עשויים להישאר עם יותר מחלקם. החידה היא להראות כיצד הם עברו את הנהר במספר המינימלי האפשרי של חציות, תוך שהם לוקחים איתם את האוצר שלהם. אין להשתמש בתחבולות, כגון חבלים, "גשרים מעופפים", זרמים, שחייה או תחבולות דומות. מקורות:

  • חֲמִשָּׁה בְּעָלִים קַנָּאִים

    בְּמַהֲלַךְ שִׁטְפוֹנוֹת מְקוֹמִיִּים מְסוּיָּמִים, חֲמִשָּׁה זוּגוֹת נְשׂוּאִים מָצְאוּ אֶת עַצְמָם מֻקָּפִים בְּמַיִם, וְהָיוּ צְרִיכִים לִבְרֹחַ מִמַּצָּבָם הַבִּלְתִּי נָעִים בְּסִירָה שֶׁיָּכְלָה לְהַכִיל רַק שְׁלֹשָׁה אֲנָשִׁים בְּכָל פַּעַם. כָּל בַּעַל הָיָה כָּל כָּךְ קַנָּא שֶׁלֹּא הָיָה מַרְשֶׁה לְאִשְׁתּוֹ לִהְיוֹת בַּסִּירָה אוֹ עַל אַחַת הַגְּדוֹת עִם גֶּבֶר אַחֵר (אוֹ עִם גְּבָרִים אֲחֵרִים) אִם הוּא עַצְמוֹ לֹא הָיָה נוֹכֵחַ. הַצִּיגוּ אֶת הַדֶּרֶךְ הַמְּהִירָה בְּיוֹתֵר לְהַעֲבִיר אֶת חֲמֵשֶׁת הָאֲנָשִׁים הָאֵלֶּה וְנְשֵׁיהֶם לְמָקוֹם מִבְטָחִים.

    קִרְאוּ לַגְּבָרִים A, B, C, D, E, וְלִנְשֵׁיהֶם הַתּוֹאֲמוֹת a, b, c, d, e. מַעֲבָר וְחֲזָרָה נֶחְשָׁבִים כִּשְׁנֵי חֲצִיּוֹת. אֵין לְהִשְׁתַּמֵּשׁ בְּטְרִיקִים כְּגוֹן חֲבָלִים, שְׂחִיָּה, זְרָמִים וְכוּ'.

    מקורות:

  • ארבע הבריחות

    קולונל ב—— היה אלמן בעל מזג שתקני מאוד. יחסו לארבע בנותיו היה חמור בצורה יוצאת דופן, כמעט אכזרי, והן באופן טבעי חשו נטייה להתרעם על כך. בהיותן נערות מקסימות בעלות כל מידה טובה והישגים רבים, אין זה מפתיע שלכל אחת היה מעריץ נלהב. אבל האב אסר על הצעירים לבקר בביתו, יירט את כל המכתבים והעמיד את בנותיו תחת פיקוח הדוק יותר מאי פעם. אבל האהבה, שלועגת למנעולים, מפתחות וחומות גן, הייתה שווה למקרה, וארבעת הצעירים קשרו קשר ותכננו בריחה כללית.

    למרגלות מדשאת הטניס בתחתית הגן זרם נהר התמזה הכסוף, ובלילה אחד, לאחר שארבע הבנות הוצאו בבטחה מחלון מעונות ל-terra firma, הן התגנבו בשקט אל גדת הנהר, שם עגנה סירה קטנה השייכת לקולונל. בעזרת זאת הם הציעו לחצות לצד הנגדי ולעשות את דרכם לסמטה שבה חיכו כלי רכב שיישאו אותם במנוסתם. אבוי! כאן, על שפת המים, החלו כבר קשייהם.

    הצעירים היו כה קנאים, שאף אחד מהם לא הרשה לארוסתו העתידית להישאר בכל עת בחברת גבר אחר, או גברים, אלא אם כן הוא עצמו נכח גם כן. כעת, הסירה יכלה להכיל רק שני אנשים, אם כי כמובן שאפשר היה לחתור בה על ידי אדם אחד, ונראה היה שאי אפשר לארבעת הזוגות לחצות אי פעם. אבל באמצע הזרם היה אי קטן, ונראה היה שהוא מציג מוצא מהקושי, משום שאפשר היה להשאיר שם אדם או אנשים בזמן שהסירה חתרה חזרה או אל הגדה הנגדית. אילו היו ערוכים לקושי שלהם, הם יכלו למצוא בקלות פתרון לבעיה הקטנה הזו בכל זמן אחר. אבל הם היו עכשיו כה ממהרים ונרגשים במנוסתם, שהבלבול שאליו נקלעו עד מהרה היה משעשע ביותר—או שהיה יכול להיות לכל אחד מלבדם.

    כתוצאה מכך, הם לקחו פי שניים זמן וחצו את הנהר פי שניים בתדירות גבוהה מהדרוש. בינתיים, הקולונל, שהיה ישן קל מאוד, חשב ששמע התזה של משוטים. הוא העלה במהירות את האזעקה בקרב בני ביתו, ונמצא שהנערות נעדרות. מישהו נשלח לתחנת המשטרה, ומספר שוטרים סייעו עד מהרה במרדף אחר הבורחים, אשר, כתוצאה מהעיכוב הזה בחציית הנהר, נתפסו במהירות. ארבע הבנות חזרו בעצב לבתיהן, ולאחר מכן ניתקו את אירוסיהן בתיעוב.

    במשך זמן רב היה זה תעלומה כיצד הצליחה קבוצת שמונת האנשים לחצות את הנהר בסירה הקטנה ההיא מבלי שאף נערה תישאר אי פעם עם גבר, אלא אם כן גם ארוסה היה נוכח. השיטה המועדפת היא לקחת שמונה אסימונים או פיסות קרטון ולסמן אותם A, B, C, D, a, b, c, d, כדי לייצג את ארבעת הגברים ואת הכלות העתידיות שלהם, ולשאת אותם מצד אחד של שולחן למשנהו בקופסת גפרורים (כדי לייצג את הסירה), כאשר מטבע מוצב באמצע השולחן כאי.

    קוראים מתבקשים כעת למצוא את השיטה המהירה ביותר להעברת המשתתפים מעבר לנהר. כמה מעברים נחוצים מיבשה ליבשה? על ידי "יבשה" מובן או חוף או אי. למרות שהסירה לא בהכרח תעגון באי בכל פעם של חציה, יש להיערך לאפשרות שזה יקרה. לדוגמה, לא יתאים שגבר יהיה לבדו בסירה (אף שהובן שהוא התכוון רק לחצות מגדה אחת לגדה הנגדית) אם במקרה הייתה נערה לבדה על האי מלבד זו שאליה היה מאורס.

    מקורות:

  • גְּנֵבַת אוֹצַר הַטִּירָה

    הַדֶּרֶךְ הַמְּתוּחְכֶּמֶת בָּהּ נִגְנְבָה תֵּבַת אוֹצָר, הַמְּכִילָה בְּעִיקָרָהּ תַּכְשִׁיטִים וַאֲבָנִים יְקָרוֹת, מִטִּירַת גְּלוּמְהֶרְסְט, עָבְרָה כְּמָסֹרֶת בְּמִשְׁפַּחַת דֶּה גּוּרְנֵי. הַגַּנָּבִים הִתְכַּלְּלוּ מֵאִישׁ, נַעַר וְיֶלֶד קָטָן, שֶׁדֶּרֶךְ הַמִּלּוּט הַיְּחִידָה שֶׁלָּהֶם עִם תֵּבַת הָאוֹצָר הָיְתָה דֶּרֶךְ חַלּוֹן גָּבוֹהַּ. מִחוּץ לַחַלּוֹן הוּצַּב גַּלְגֶּלֶת, שֶׁעָלֶיהָ עָבַר חֶבֶל עִם סַל בְּכָל קָצֶה. כְּשֶׁסַּל אֶחָד הָיָה עַל הַקַּרְקַע, הַשֵּׁנִי הָיָה בַּחַלּוֹן. הַחֶבֶל סֻדַּר כָּךְ שֶׁהָאֲנָשִׁים בַּסַּל לֹא יָכְלוּ לַעֲזֹר לְעַצְמָם בְּאֶמְצָעוּתוֹ וְלֹא לְקַבֵּל עֶזְרָה מֵאֲחֵרִים. בְּקִצּוּר, הַדֶּרֶךְ הַיְּחִידָה לְשִׁמּוּשׁ בַּסַּלִּים הָיְתָה עַל יְדֵי הַצָּבַת מִשְׁקָל כָּבֵד יוֹתֵר בְּאֶחָד מֵהַשֵּׁנִי.

    עַכְשָׁו, מִשְׁקַל הָאִישׁ הָיָה `195` לִיבְּרוֹת, הַנַּעַר `105` לִיבְּרוֹת, הַיֶּלֶד `90` לִיבְּרוֹת וְתֵּבַת הָאוֹצָר `75` לִיבְּרוֹת. הַמִּשְׁקָל בַּסַּל הַיּוֹרֵד לֹא יָכֹל לַחְרֹג מִזֶּה שֶׁבַּשֵּׁנִי בְּיוֹתֵר מִ `15` לִיבְּרוֹת בְּלִי לִגְרֹם לִירִידָה כֹּה מְהִירָה שֶׁתִּהְיֶה מְסֻכֶּנֶת בְּיוֹתֵר לְבֶן אָדָם, אַף עַל פִּי שֶׁלֹּא תִּגְרֹם נֶזֶק לָרְכוּשׁ הַגָּנוּב. רַק שְׁנֵי אֲנָשִׁים, אוֹ אָדָם אֶחָד וְהָאוֹצָר, יָכְלוּ לְהָנִיחַ בְּאוֹתוֹ סַל בְּבַת אַחַת. אֵיךְ הֵם הִצְלִיחוּ לִבְרֹחַ וְלָקַחַת אִתָּם אֶת תֵּבַת הָאוֹצָר?

    הַחִידָה הִיא לִמְצֹא אֶת הַדֶּרֶךְ הַקְּצָרָה בְּיוֹתֵר לְבִצּוּעַ הַמַּעֲשֶׂה, שֶׁכְּשֶׁעַצְמוֹ אֵינוֹ קָשֶׁה. זִכְרוּ, אָדָם לֹא יָכוֹל לַעֲזֹר לְעַצְמוֹ עַל יְדֵי תְּלִיָּה עַל הַחֶבֶל, הַדֶּרֶךְ הַיְּחִידָה הִיא לָרֶדֶת "עִם מַהֲלוּמָה," כְּשֶׁהַמִּשְׁקָל בַּסַּל הַשֵּׁנִי כְּמִשְׁקָל נֶגְדִּי.

    מקורות:

  • דומינו בסדרה

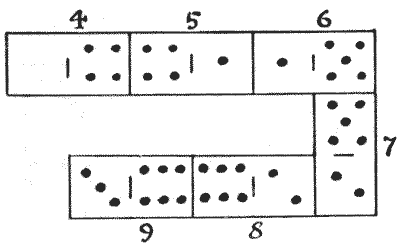    ניתן לראות ששיחקתי שישה אבני דומינו, באיור, בהתאם לכללים הרגילים של המשחק, `4` נגד `4, 1` נגד `1`, וכן הלאה, ועדיין סכום הנקודות על אבני הדומינו העוקבות, `4, 5, 6, 7, 8, 9`, נמצא בסדרה חשבונית; כלומר, למספרים שנלקחו לפי הסדר יש הפרש קבוע של `1`. בכמה דרכים שונות נוכל לשחק שישה אבני דומינו, מקופסה רגילה של עשרים ושמונה, כך שהמספרים עליהם יהיו בסדרה חשבונית? אנחנו תמיד חייבים לשחק משמאל לימין, ומספרים בסדרה חשבונית יורדת (כגון `9, 8, 7, 6, 5, 4`) אינם קבילים. מקורות:

  • חמש אבני דומינו

     

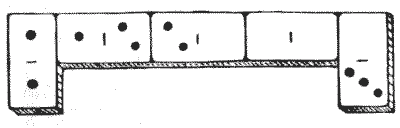
    הנה חידה קטנה חדשה שאינה קשה, אך כנראה תמצא חן בעיני הקוראים שלי. ניתן לראות שחמש אבני הדומינו מסודרות ברצף נכון (כלומר, עם `1` כנגד `1, 2` כנגד `2`, וכן הלאה), כך שהמספר הכולל של הנקודות בשתי אבני הדומינו הקיצוניות הוא חמש, וסכום הנקודות בשלוש אבני הדומינו באמצע הוא גם חמש. ישנן רק שלוש סידורים אחרים שנותנים חמש עבור הסכומים. הם: —

    (1—0) (0—0) (0—2) (2—1) (1—3)
    (4—0) (0—0) (0—2) (2—1) (1—0)
    (2—0) (0—0) (0—1) (1—3) (3—0)

    עכשיו, כמה סידורים דומים יש לחמש אבני דומינו שייתנו שש במקום חמש בשני הסכומים?

    מקורות:

  • פאזל מסגרת הדומינו

    ניתן לראות באיור שהסט המלא של עשרים ושמונה אבני הדומינו מסודר בצורת מסגרת מרובעת, כאשר `6` מול `6, 2` מול `2`, ריק מול ריק, וכן הלאה, כמו במשחק. יתגלה כי הנקודות בשורה העליונה ובטור השמאלי מסתכמות ל-`44`. הנקודות בשני הצדדים האחרים מסתכמות ל-`59` ו-`32` בהתאמה. הפאזל הוא לסדר מחדש את אבני הדומינו באותה צורה כך שכל ארבעת הצדדים יסתכמו ל-`44`. זכור שאבני הדומינו חייבות להיות מונחות נכון אחת מול השנייה כמו במשחק. מקורות:

  • פאזל מסגרת הקלפים

    באיור יש לנו מסגרת הבנויה מעשרה קלפי משחק, אס עד עשר יהלום. הילדים שהכינו אותה רצו שהנקודות ניקוד בכל ארבעת הצדדים יסתכמו באופן שווה, אבל הם נכשלו בניסיונם וויתרו עליה כבלתי אפשרית. ניתן לראות שהנקודות בשורה העליונה, בשורה התחתונה ובצד שמאל מסתכמות כולן ב-`14`, אבל הצד הימני מסתכם ב-`23`. עכשיו, מה שהם ניסו לעשות הוא די אפשרי. האם אתה יכול לסדר מחדש את עשרת הקלפים באותה תצורה כך שכל ארבעת הצדדים יסתכמו באופן שווה? כמובן שהם לא צריכים להסתכם ב-`14`, אלא בכל מספר שתבחר.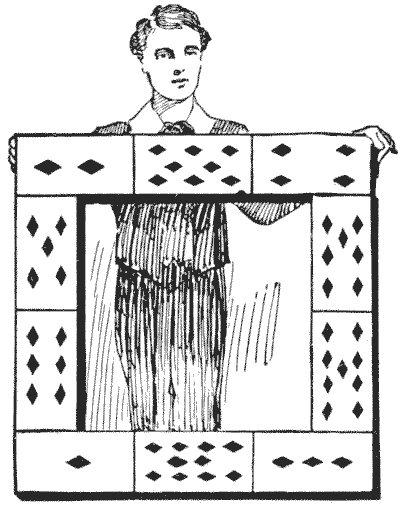 מקורות:

  • צלב הקלפים

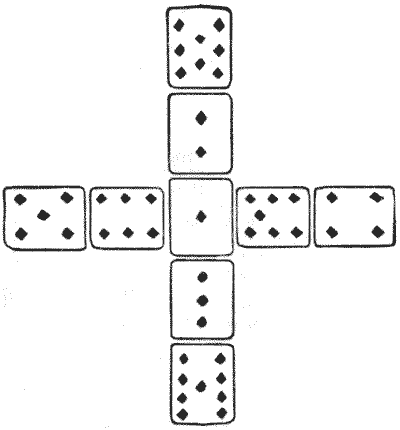    במקרה זה אנו משתמשים רק בתשעה קלפים - האס עד תשע יהלומים. החידה היא לסדר אותם בצורת צלב, בדיוק כפי שמוצג באיור, כך שהנקודות בפס האנכי ובפס האופקי יסתכמו באופן שווה. בדוגמה הנתונה, ניתן לראות ששני הכיוונים מסתכמים ל-`23`. מה שאני רוצה לדעת הוא, כמה דרכים שונות יש לסדר מחדש את הקלפים כדי להגיע לתוצאה זו? ניתן לראות כי, מבלי להשפיע על הפתרון, אנו יכולים להחליף את ה-`5` עם ה-`6`, את ה-`5` עם ה-`7`, את ה-`8` עם ה-`3`, וכן הלאה. כמו כן, אנו יכולים לגרום לפסים האופקי והאנכי להחליף מקומות. אבל מניפולציות ברורות כאלה אינן נחשבות לפתרונות שונים. כולן וריאציות בלבד של פתרון יסודי אחד. עכשיו, כמה פתרונות שונים באופן מהותי כאלה יש? הנקודות לא צריכות, כמובן, תמיד להסתכם ל-`23`. מקורות: