שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 381 - פאזל מסגרת הקלפים

    באיור יש לנו מסגרת הבנויה מעשרה קלפי משחק, אס עד עשר יהלום. הילדים שהכינו אותה רצו שהנקודות ניקוד בכל ארבעת הצדדים יסתכמו באופן שווה, אבל הם נכשלו בניסיונם וויתרו עליה כבלתי אפשרית. ניתן לראות שהנקודות בשורה העליונה, בשורה התחתונה ובצד שמאל מסתכמות כולן ב-`14`, אבל הצד הימני מסתכם ב-`23`. עכשיו, מה שהם ניסו לעשות הוא די אפשרי. האם אתה יכול לסדר מחדש את עשרת הקלפים באותה תצורה כך שכל ארבעת הצדדים יסתכמו באופן שווה? כמובן שהם לא צריכים להסתכם ב-`14`, אלא בכל מספר שתבחר.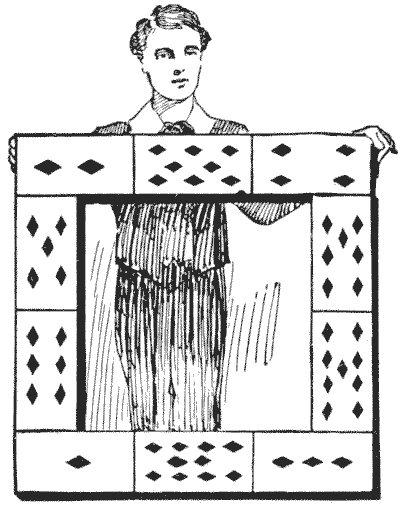

  • שאלה 382 - צלב הקלפים

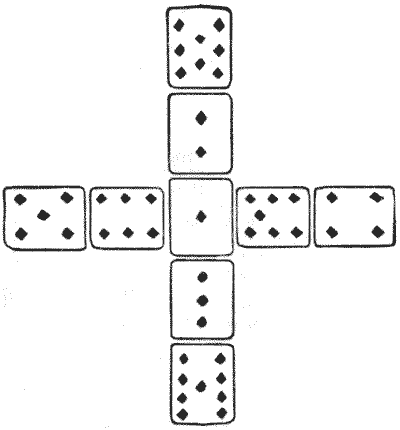    במקרה זה אנו משתמשים רק בתשעה קלפים - האס עד תשע יהלומים. החידה היא לסדר אותם בצורת צלב, בדיוק כפי שמוצג באיור, כך שהנקודות בפס האנכי ובפס האופקי יסתכמו באופן שווה. בדוגמה הנתונה, ניתן לראות ששני הכיוונים מסתכמים ל-`23`. מה שאני רוצה לדעת הוא, כמה דרכים שונות יש לסדר מחדש את הקלפים כדי להגיע לתוצאה זו? ניתן לראות כי, מבלי להשפיע על הפתרון, אנו יכולים להחליף את ה-`5` עם ה-`6`, את ה-`5` עם ה-`7`, את ה-`8` עם ה-`3`, וכן הלאה. כמו כן, אנו יכולים לגרום לפסים האופקי והאנכי להחליף מקומות. אבל מניפולציות ברורות כאלה אינן נחשבות לפתרונות שונים. כולן וריאציות בלבד של פתרון יסודי אחד. עכשיו, כמה פתרונות שונים באופן מהותי כאלה יש? הנקודות לא צריכות, כמובן, תמיד להסתכם ל-`23`.

  • שאלה 383 - חידת קלף ה-"T"

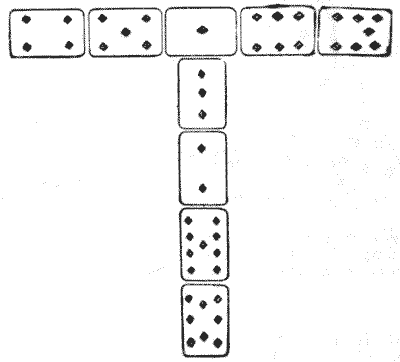    חידה משעשעת עם קלפים היא לקחת את תשעת הקלפים מסדרה אחת, מאס ועד תשע כולל, ולסדר אותם בצורת האות "T," כפי שמוצג באיור, כך שהנקודות בשורה האופקית יספרו אותו דבר כמו אלו בעמודה. בדוגמה הנתונה הם מסתכמים לעשרים ושלוש בשני הכיוונים. עכשיו, זה די קל להשיג סידור נכון יחיד. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת. למרות שהמספר גבוה, הפתרון לא באמת קשה אם נתקוף את החידה בצורה הנכונה. את הדרך ההפוכה המתקבלת על ידי שיקוף האיור במראה לא נספור כשונה, אך כל שאר השינויים במיקומים היחסיים של הקלפים ייספרו כאן. כמה דרכים שונות יש?

  • שאלה 384 - משולשי קלפים

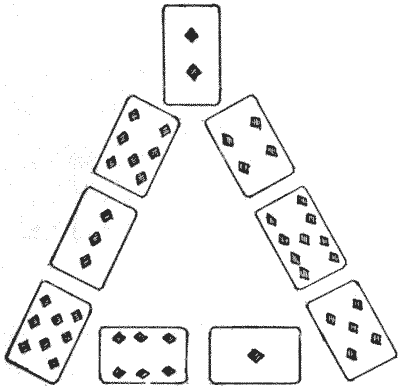
    כאן עליך לבחור את תשעת הקלפים, אס עד תשע יהלומים, ולסדר אותם בצורת משולש, בדיוק כפי שמוצג באיור, כך שהנקודות יסתכמו לאותו דבר בכל שלושת הצדדים. בדוגמה הנתונה ניתן לראות שהם מסתכמים ל-`20` בכל צד, אך למספר המסוים אין חשיבות כל עוד הוא זהה בכל שלושת הצדדים. החידה היא לגלות בכמה דרכים שונות ניתן לעשות זאת.

    אם פשוט תסובב את הקלפים כך שאחד משני הצדדים האחרים יהיה הכי קרוב אליך, זה לא ייחשב שונה, כי הסדר יהיה זהה. כמו כן, אם תחליף את המקומות של `4, 9, 5` עם `7, 3, 8`, ובאותו הזמן תחליף את `1` ו-`6`, זה לא יהיה שונה. אבל אם רק תחליף את `1` ו-`6`, זה יהיה שונה, כי הסדר סביב המשולש אינו זהה. הסבר זה ימנע כל ספק לגבי התנאים.

  • שאלה 385 - "STRAND" סבלנות

    הרעיון לכך עלה לי כששקלתי את משחק הסבלנות שנתתי בתוך Strand Magazine לחודש דצמבר, `1910`, אשר הודפס מחדש בספרו השני של ארנסט ברגהולט Second Book of Patience Games, תחת השם החדש "המלך אלברט".

    צרו שתי ערימות קלפים באופן הבא: `9` יהלום, `8` עלה, `7` יהלום, `6` עלה, `5` יהלום, `4` עלה, `3` יהלום, `2` עלה, `1` יהלום, ו-`9` תלתן, `8` תלתן, `7` תלתן, `6` תלתן, `5` תלתן, `4` תלתן, `3` תלתן, `2` תלתן, `1` תלתן, כאשר ה-`9` של יהלומים בתחתית ערימה אחת וה-`9` של תלתן בתחתית הערימה האחרת. המטרה היא להחליף את העלים עם התלתנים, כך שהיהלומים והתלתנים עדיין יהיו בסדר מספרי בערימה אחת והתלתנים והעלים בערימה השנייה. ישנם ארבעה מקומות פנויים בנוסף לשני המקומות שתפוסים על ידי הערימות, וניתן להניח כל קלף על מקום פנוי, אבל ניתן להניח קלף רק על קלף אחר בעל ערך גבוה יותר הבא אחריו — אס על שתיים, שתיים על שלוש וכן הלאה. נדרשת סבלנות כדי לגלות את הדרך הקצרה ביותר לעשות זאת. כאשר ישנם ארבעה מקומות פנויים, ניתן לערום ארבעה קלפים בשבעה מהלכים, עם שלושה מקומות בלבד ניתן לערום אותם בתשעה מהלכים, ועם שני מקומות אי אפשר לערום יותר משני קלפים. כאשר יש לך תפיסה של עובדות אלה ודומות להן, תוכל להסיר מספר קלפים בשלמותם ולרשום `7, 9`, או כל מספר המהלכים הנדרש. הקיצור ההדרגתי של המשחק הוא מרתק, והניסיונות הראשונים הם ארוכים באופן מפתיע.

  • שאלה 386 - טריק עם קוביות

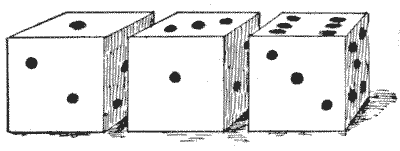    הנה טריק קטן ונחמד עם שלוש קוביות. אני מבקש ממך לזרוק את הקוביות מבלי שאראה אותן. לאחר מכן אני אומר לך להכפיל את הנקודות של הקוביה הראשונה ב-`2` ולהוסיף `5`; ואז להכפיל את התוצאה ב-`5` ולהוסיף את הנקודות של הקוביה השנייה; ואז להכפיל את התוצאה ב-`10` ולהוסיף את הנקודות של הקוביה השלישית. לאחר מכן אתה נותן לי את הסכום הכולל, ואני יכול מיד לומר לך את הנקודות שנזרקו בשלוש הקוביות. איך אני עושה את זה? לדוגמה, אם זרקת `1, 3`, ו-`6`, כפי שמוצג באיור, התוצאה שהיית נותן לי תהיה `386`, שממנה אוכל מיד לומר מה זרקת.

  • שאלה 387 - משחק קריקט בכפר

    במשחק קריקט, Dingley Dell v. All Muggleton, האחרון קיבל את הסיבוב הראשון. מר דמפקינס ומר פודר היו בשערים, כאשר דמפקינס הזהיר ביצע חיתוך מאוחר מרהיב, ומר פודר קרא לו לרוץ. ארבע ריצות הושלמו לכאורה, אך השופטים הערניים בכל קצה קראו, "שלוש חסרות," מה שהפך לשש ריצות חסרות בסך הכל. איזה מספר השיג מר דמפקינס? כאשר Dingley Dell קיבלו את תורם בשערים, האלופים שלהם היו מר לאפי ומר סטראגלס. האחרון ביצע נסיעה מרהיבה מהצד, והזמין את עמיתו "לבוא," וכתוצאה מכך הצופים הבחינו ומחאו כפיים על מה שהיה אמור להיות שלוש ריצות חדות. אבל השופטים הצהירו שהיו שתי ריצות חסרות בכל קצה - ארבע בסך הכל. באיזו מידה, אם בכלל, התמרון הזה הגדיל את סך הנקודות של מר סטראגלס?

  • שאלה 388 - צרצר איטי

    במשחק המחוז האחרון בין ווסקס לנינקומשייר, הקבוצה הראשונה הייתה על המגרש כל היום, השחקן האחרון הוצא כמה דקות לפני הזמן לסיום המשחק. המשחק היה כל כך איטי שרוב הצופים נרדמו עמוק, וכשהתעוררו על ידי אחד הפקידים שפינה את השטח, למדנו ששני שחקנים הוצאו בפסיקה לג-בפור-וויקט עם ציון משולב של `19` ריצות; ארבעה שחקנים נתפסו עם ציון משולב של `17` ריצות; שחקן אחד הודח בריצה עם ניקוד אפס; והשאר הודחו באמצעות באולינג עבור `3` ריצות כל אחד. לא היו תוספות. לא נאמר לנו מי מהשחקנים היה הקפטן, אבל הוא השיג בדיוק `15` יותר מהממוצע של הקבוצה שלו. מה היה הניקוד של הקפטן?

  • שאלה 389 - שחקני הכדורגל

    "זהו משחק נפלא!" נשמע חובב נלהב קורא. "בסיום העונה שעברה, מבין שחקני הכדורגל שאני מכיר, לארבעה נשברה זרוע שמאל, לחמישה נשברה זרוע ימין, לשניים זרוע ימין הייתה בריאה, ולשלושה זרוע שמאל הייתה בריאה." האם תוכלו לגלות מההצהרה הזו מהו המספר הקטן ביותר של שחקנים שהדובר יכול היה להכיר?

    כלל לא נובע מכך שהיו ארבעה עשר אנשים, מכיוון שלדוגמה, שניים מהאנשים ששברו את זרוע שמאל יכולים להיות גם שניים מאלה שהייתה להם זרוע ימין בריאה.

  • שאלה 390 - חידת מרוץ הסוסים

    אין מוסר בחידות. כאשר אנו פותרים את החידה הישנה על הקברניט שנאלץ להשליך חצי מצוותו מעבר לסיפון בסערה, והסכים לערוך הגרלה, אך סידר את האנשים כך שרק הטורקים הוקרבו, וכל הנוצרים נותרו על הסיפון, איננו עוצרים לדון במוסריות המפוקפקת של ההליך. וכאשר אנו עוסקים בבעיית מדידה, שבה צליינים צמאים מסוימים אמורים לערוך חלוקה הוגנת של חבית בירה, איננו מתנגדים לכך, כמנועים מוחלטים, שזה מנוגד למצפוננו להתעסק עם משקאות משכרים. לכן איני מתנצל על הצגת חידה העוסקת בהימורים.

    שלושה סוסים—בלוט, כחול-בקבוק וקפסולה—מתחילים במרוץ. יחסי ההימורים הם `4` ל-`1`, בלוט; `3` ל-`1`, כחול-בקבוק; `2` ל-`1`, קפסולה. עכשיו, כמה עלי להשקיע על כל סוס כדי לזכות ב-£`13`, לא משנה איזה סוס יגיע ראשון? נניח, לדוגמה, שהימרתי £`5` על כל סוס. אז, אם בלוט ינצח, אקבל £`20` (ארבע פעמים £`5`), ואצטרך לשלם £`5` עבור כל אחד משני הסוסים האחרים; ובכך אזכה ב-£`10`. אבל יתברר שאם כחול-בקבוק יהיה ראשון אזכה רק ב-£`5`, ואם קפסולה תנצח לא ארוויח דבר ולא אפסיד דבר. זה יבהיר את השאלה לחלוטין למתחילים, שכמוני, לא מתעניינים בקריאה של האחווה שמצהירה שהיא עוסקת במשימה הנאצלת של "שיפור גזע הסוסים".