שעשועונים במתמטיקה, הנרי ארנסט דודני
-
שאלה 391 - מרוץ המכוניות
לפעמים הצהרה פשוטה למדי, אם מנוסחת באופן לא מוכר, תגרום למבוכה ניכרת. הנה דוגמה, וללא ספק היא תבלבל קצת את חלק מקוראי הצעירים יותר שלי. במקרה הייתי במרוץ מכוניות בברוקלנדס, כשצופה אחד אמר למשנהו, בזמן שמספר מכוניות הסתובבו סביב המסלול המעגלי:—
"הנה גוגלסמית'—האיש הזה במכונית הלבנה!"
"כן, אני רואה," הייתה התשובה; "אבל כמה מכוניות רצות במרוץ הזה?"
אז באה התשובה המוזרה הזו:—
"שליש מהמכוניות שלפני גוגלסמית' ועוד שלושה רבעים מאלה שמאחוריו יתנו לך את התשובה."
עכשיו, האם אתה יכול לומר כמה מכוניות רצו במרוץ?
-
שאלה 392 - משחק החלוקים
הנה משחק חידה קטן ומעניין שנהגתי לשחק עם מכר על החוף בסלוקומב-און-סי. שני שחקנים מניחים מספר אי זוגי של חלוקים, נניח חמישה עשר, ביניהם. לאחר מכן כל אחד בתורו לוקח אחד, שניים או שלושה חלוקים (כפי שהוא בוחר), והמנצח הוא זה שמקבל מספר אי זוגי. לכן, אם אתה מקבל שבע והיריב שלך שמונה, אתה מנצח. אם אתה מקבל שש והוא מקבל תשע, הוא מנצח. האם השחקן הראשון או השני אמור לנצח, וכיצד? לאחר שפתרתם את השאלה עם חמישה עשר חלוקים, נסו שוב עם, למשל, שלושה עשר. -
שאלה 393 - שני הצריחים
זוהי משחק חידה לשני שחקנים. לכל שחקן יש צריח אחד. השחקן הראשון מניח את הצריח שלו על כל משבצת בלוח שהוא בוחר, ואז השחקן השני עושה את אותו הדבר. עכשיו הם משחקים בתורות, כאשר המטרה של כל תור היא ללכוד את הצריח של היריב. אבל במשחק הזה אי אפשר לשחק דרך קו תקיפה מבלי להילכד. כלומר, אם בתרשים זה תורו של השחור לשחק, הוא לא יכול להזיז את הצריח שלו למשבצת של הפרש של המלך שלו, או למשבצת של הצריח של המלך שלו, כי הוא ייכנס ל"קו האש" כשהוא עובר על פני המשבצת של הרץ של המלך שלו. מאותה סיבה הוא לא יכול לעבור לצריח של המלכה שלו במשבצת השביעית או השמינית. עכשיו, המשחק לעולם לא יכול להסתיים בתיקו. במוקדם או במאוחר אחד הצריחים חייב ליפול, אלא אם כן, כמובן, שני השחקנים מבצעים את האבסורד של לא לנסות לנצח. הטריק לנצח הוא פשוט להפליא כשאתה יודע אותו. האם אתה יכול לפתור את החידה? נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון קומבינטוריקה -> צביעות -> צביעת שחמט
נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון קומבינטוריקה -> צביעות -> צביעת שחמט -
שאלה 394 - חתול בפינה
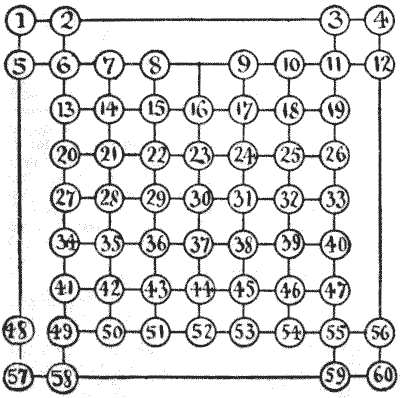
גרסה זו של החידה האחרונה משוחקת גם היא על ידי שני אנשים. אחד מניח כלי משחק על מספר `6`, והשני מניח כלי משחק על מספר `55`, והם משחקים בתורות על ידי הזזת הכלי לכל מספר אחר בקו. אם היריב שלך עובר בכל עת לאחד הקווים שאתה תופס, או אפילו חוצה אחד מהקווים שלך, אתה מיד לוכד אותו ומנצח. ניקח משחק המחשה.
א' זז מ-`55` ל-`52`; ב' זז מ-`6` ל-`13`; א' מתקדם ל-`23`; ב' הולך ל-`15`; א' נסוג ל-`26`; ב' נסוג ל-`13`; א' מתקדם ל-`21`; ב' נסוג ל-`2`; א' מתקדם ל-`7`; ב' הולך ל-`3`; א' זז ל-`6`; ב' חייב כעת ללכת ל-`4`; א' מתבסס ב-`11`, ויש ללכוד את ב' במהלך הבא מכיוון שהוא נאלץ לחצות קו שעליו עומד א'. שחקו זאת שוב ותבינו את המשחק ישירות. כעת, החלק החידתי של המשחק הוא זה: איזה שחקן צריך לנצח, וכמה מהלכים נחוצים?
נושאים:קומבינטוריקה -> תורת המשחקים -
שאלה 395 - משחק חידה מלחמתי
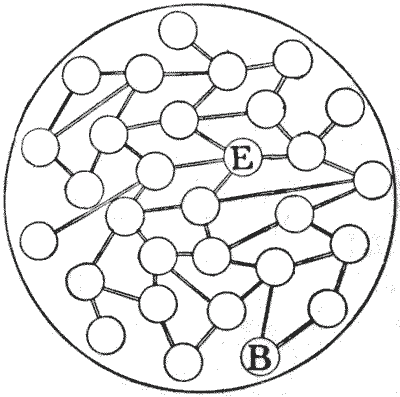 הנה עוד משחק חידה. שחקן אחד, המייצג את הגנרל הבריטי, מניח כלי בנקודה B, והשחקן השני, המייצג את האויב, מניח את הכלי שלו בנקודה E. הבריטי עושה את ההתקדמות הראשונה לאורך אחת הדרכים לעיר הבאה, ואז האויב עובר לאחת הערים הקרובות אליו, וכן הלאה בתורות, עד שהגנרל הבריטי מגיע לאותה עיר כמו האויב ולוכד אותו. למרות שכל אחד חייב תמיד לנוע לאורך דרך לעיר הבאה בלבד, והשחקן השני רשאי לעשות כמיטב יכולתו כדי להימנע מלכידה, הגנרל הבריטי (כפי שאנו אמורים להניח, מהאנלוגיה של החיים האמיתיים) חייב לנצח ללא טעות. אבל איך? זאת השאלה.
נושאים:קומבינטוריקה -> תורת המשחקים
הנה עוד משחק חידה. שחקן אחד, המייצג את הגנרל הבריטי, מניח כלי בנקודה B, והשחקן השני, המייצג את האויב, מניח את הכלי שלו בנקודה E. הבריטי עושה את ההתקדמות הראשונה לאורך אחת הדרכים לעיר הבאה, ואז האויב עובר לאחת הערים הקרובות אליו, וכן הלאה בתורות, עד שהגנרל הבריטי מגיע לאותה עיר כמו האויב ולוכד אותו. למרות שכל אחד חייב תמיד לנוע לאורך דרך לעיר הבאה בלבד, והשחקן השני רשאי לעשות כמיטב יכולתו כדי להימנע מלכידה, הגנרל הבריטי (כפי שאנו אמורים להניח, מהאנלוגיה של החיים האמיתיים) חייב לנצח ללא טעות. אבל איך? זאת השאלה.
נושאים:קומבינטוריקה -> תורת המשחקים -
שאלה 396 - תעלומת גפרורים
הנה משחק קטן שתנאיו פשוטים באופן ילדותי. אבל הוא ראוי לחקירה.
מר סטאבס משך שולחן קטן בינו לבין חברו, מר וילסון, ולקח קופסת גפרורים, שממנה ספר שלושים.
"הנה שלושים גפרורים," אמר. "אני מחלק אותם לשלוש ערימות לא שוות. תן לי לראות. יש לנו `14, 11` ו-`5`, במקרה. עכשיו, שני השחקנים מושכים לסירוגין כל מספר מכל ערימה אחת, ומי שמושך את הגפרור האחרון מפסיד במשחק. זה הכל! אני אשחק איתך, וילסון. הרכבתי את הערימות, אז יש לך את התור הראשון."
"מכיוון שאני יכול למשוך כל מספר," אמר מר וילסון, "נניח שאני מציג את המתינות הרגילה שלי ואקח את כל ערימת ה-`14`."
"זה הכי גרוע שיכולת לעשות, כי זה מפסיד מיד. אני לוקח `6` מה-`11`, ומשאיר שתי ערימות שוות של `5`, ולהשאיר שתי ערימות שוות זה ניצחון בטוח (פרט לחריג היחיד של `1, 1`), כי מה שלא תעשה בערימה אחת אני יכול לחזור עליו בשנייה. אם אתה משאיר `4` בערימה אחת, אני משאיר `4` בשנייה. אם אתה משאיר רק `1` בערימה אחת, אז אני לוקח את כל הערימה השנייה. אם אתה לוקח את כל הערימה האחת, אני לוקח את הכל מלבד אחד בשנייה. לא, אסור לך אף פעם להשאיר שתי ערימות, אלא אם כן הן ערימות שוות ויותר מ-`1, 1`. בוא נתחיל שוב."
"בסדר גמור," אמר מר וילסון. "אני אקח `6` מה-`14`, ואשאיר לך `8, 11, 5`."
מר סטאבס אז השאיר `8, 11, 3`; מר וילסון, `8, 5, 3`; מר סטאבס, `6, 5, 3`; מר וילסון, `4, 5, 3`; מר סטאבס, `4, 5, 1`; מר וילסון, `4, 3, 1`; מר סטאבס, `2, 3, 1`; מר וילסון, `2, 1, 1`; שאותו מר סטאבס צמצם ל-`1, 1, 1`.
"עכשיו ברור לחלוטין שאני חייב לנצח," אמר מר סטאבס, כי אתה חייב לקחת `1`, ואז אני לוקח `1`, ומשאיר לך את הגפרור האחרון. אף פעם לא היה לך סיכוי. יש בדיוק שלושה עשר דרכים שונות שבהן ניתן לקבץ את הגפרורים בהתחלה לניצחון בטוח. למעשה, הקבוצות שנבחרו, `14, 11, 5`, הן ניצחון בטוח, כי על מה שהיריב שלך ישחק יש קבוצה מנצחת אחרת שאתה יכול להבטיח, וכך הלאה עד הגפרור האחרון."
נושאים:קומבינטוריקה -> תורת המשחקים -
שאלה 397 - משחק הקוביות המונטנגרי
מסופר כי לתושבי מונטנגרו יש משחק קוביות קטן שהוא גם גאוני וגם ראוי לחקירה. שני השחקנים בוחרים תחילה שני זוגות שונים של מספרים אי-זוגיים (תמיד גבוהים מ-`3`), ואז מטילים לסירוגין שלוש קוביות. מי שמטיל ראשון את הקוביות כך שסכומן הוא אחד מהמספרים שבחר מנצח. אם שניהם מצליחים בשתי הטלות עוקבות, זה תיקו והם מנסים שוב. לדוגמה, שחקן אחד יכול לבחור `7` ו-`15` והשני `5` ו-`13`. לאחר מכן, אם השחקן הראשון מטיל כך ששלוש הקוביות מסתכמות ל-`7` או `15`, הוא מנצח, אלא אם כן השחקן השני מקבל `5` או `13` בהטלה שלו.
החידה היא לגלות אילו שני זוגות מספרים יש לבחור כדי לתת לשני השחקנים סיכוי שווה בדיוק.
-
שאלה 398 - חידת הסיגר
הצעתי פעם את החידה הבאה במועדון לונדוני, ולתקופה ניכרת היא ספגה את תשומת הלב של החברים. הם לא הצליחו להבין אותה, וחשבו שהיא בלתי אפשרית לפתרון. ובכל זאת, כפי שאראה, התשובה פשוטה להפליא.
שני אנשים יושבים ליד שולחן מרובע. אחד מניח סיגר רגיל (שטוח בקצה אחד, מחודד בקצה השני) על השולחן, ואז השני עושה את אותו הדבר, וכן הלאה לסירוגין, בתנאי שאף סיגר לא יגע באחר. איזה שחקן יצליח להניח את הסיגר האחרון, בהנחה שכל אחד מהם ישחק בצורה הטובה ביותר האפשרית? גודל פני השולחן וגודל הסיגר אינם נתונים, אך כדי לשלול את התשובה המגוחכת שהשולחן עשוי להיות כה קטן עד שהוא יכול להכיל רק סיגר אחד, נאמר שהשולחן לא יהיה קטן מ- `2` רגל מרובע והסיגר לא יותר מ- `4`½ אינץ' אורך. עם ההגבלות האלה אתה יכול לקחת כל מימד שתרצה. כמובן שאנו מניחים שכל הסיגרים זהים לחלוטין בכל מובן. האם השחקן הראשון או השחקן השני ינצח?
-
שאלה 399 - השמונה הבעייתית
כמעט כולם יודעים ש"ריבוע קסם" הוא סידור של מספרים בצורת ריבוע כך שכל שורה, כל טור וכל אחד משני האלכסונים הארוכים מסתכמים באופן שווה. לדוגמה, לא תתקשו במיוחד פשוט להציב מספר שונה בכל אחד מתשעת התאים באיור כך שהשורות, הטורים והאלכסונים יסתכמו כולם ל-`15`. ובניסיון הראשון שלכם סביר להניח שתגלו שיש לכם `8` באחת הפינות. החידה היא לבנות את ריבוע הקסם, תחת אותם תנאים, עם `8` במיקום המוצג.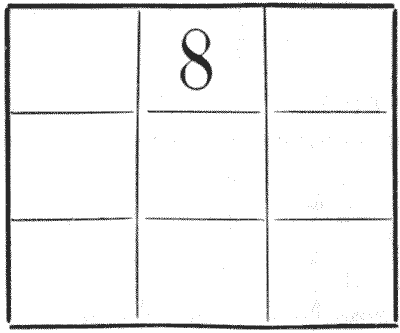 נושאים:קומבינטוריקה -> טבלאות מספריות
נושאים:קומבינטוריקה -> טבלאות מספריות -
שאלה 400 - רצועות הקסם

קרה שהיו מונחות על השולחן שלי מספר רצועות קרטון, ועליהן מודפסים מספרים מ-`1` ומעלה בסדר עולה. עלה בי הרעיון לפתע, כפי שלרעיונות יש נטייה להופיע באופן בלתי צפוי, ליצור חידה קטנה. אני תוהה אם קוראים רבים יגיעו לאותו פתרון שאני הגעתי אליו.
קחו שבע רצועות קרטון והניחו אותן יחד כפי שמוצג לעיל. לאחר מכן כתבו על כל אחת מהן את המספרים `1, 2, 3, 4, 5, 6, 7`, כפי שמוצג, כך שהמספרים ייצרו שבע שורות ושבע עמודות.
כעת, החידה היא לחתוך את הרצועות הללו למספר המועט ביותר של חלקים, כך שניתן יהיה להניח אותם יחד וליצור ריבוע קסם, כאשר שבע השורות, שבע העמודות ושני האלכסונים מסתכמים לאותו מספר. אסור להפוך או להניח אף ספרה על צידה — כלומר, כל הרצועות חייבות להיות מונחות בכיוון המקורי שלהן.
כמובן שאפשר לחתוך כל רצועה לשבעה חלקים נפרדים, כאשר כל חלק מכיל מספר, והחידה תהיה קלה מאוד, אבל אני לא צריך לומר שארבעים ותשעה חלקים רחוקים מאוד מלהיות המספר המועט ביותר האפשרי.