שעשועונים במתמטיקה, הנרי ארנסט דודני

  • שאלה 401 - שמונה אסירים עליזים

     

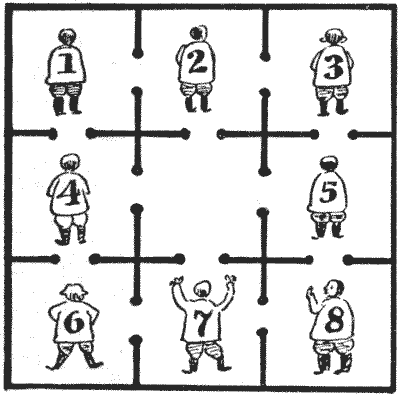
    האיור מציג תוכנית של בית סוהר המכיל תשעה תאים, כולם מקושרים זה לזה באמצעות פתחי דלתות. לשמונת האסירים יש מספרים על גבם, ומותר לכל אחד מהם להתעמל בכל תא שמתפנה, בכפוף לכלל שבאף זמן נתון לא יהיו שני אסירים באותו תא. המלך העליז שבתחום שלטונו היה ממוקם בית הסוהר הציע להם נוחיות מיוחדות בערב חג המולד אחד, אם, מבלי להפר את הכלל הזה, הם יוכלו למקם את עצמם כך שמספריהם ייצרו ריבוע קסם.

    כעת, לאסיר מספר `7` היה ידע רב על ריבועי קסם, ולכן הוא פיתח תוכנית ובחר באופן טבעי בשיטה המהירה ביותר—כלומר, כזו הכוללת את המספר הקטן ביותר האפשרי של מעברים מתא לתא. אבל אחד האנשים היה ממורמר, עקשן (בלתי מתאים לחלוטין לחברתם של חבריו העליזים), והוא סירב לצאת מתאו או לקחת חלק כלשהו בהליכים. אבל מספר `7` היה שווה ערך לחלוטין למצב החירום, וגילה שהוא עדיין יכול לעשות את מה שנדרש במספר המועט ביותר האפשרי של מהלכים, מבלי להטריד את הבהמה לעזוב את תאו. החידה היא להראות איך הוא עשה זאת, ואגב כך, לגלות איזה אסיר היה טיפש ועקשן כל כך. האם תוכלו למצוא את הבחור?

  • שאלה 402 - תִשְׁעָה אסִירִים עַלִיזִים

    זמן קצר לאחר התקרית שתועדה בחידה הקודמת, אסיר תשיעי הוכנס לתא הריק, והמלך העליז הציע להם חירות מוחלטת בתנאים המוזרים הבאים. הם נדרשו לסדר את עצמם מחדש בתאים כך שהמספרים שלהם יצרו ריבוע קסם מבלי שהתנועות שלהם יגרמו לשניים מהם להיות אי פעם באותו תא יחד, למעט שבתחילה מותר לאדם אחד להיות מונח על כתפיו של אדם אחר, ובכך להוסיף את המספרים שלהם יחד, ולנוע כאדם אחד. לדוגמה, מס' `8` עשוי להיות מונח על כתפיו של מס' `2`, ואז הם ינועו יחד כ-`10`. על הקורא לנסות תחילה לפתור את החידה במספר המהלכים המועט ביותר האפשרי, ואז לוודא שלאדם שעליו הוטל הנטל יש את כמות העבודה הקטנה ביותר האפשרית.

  • שאלה 403 - הצינוק הספרדי

    לא רחוק מחמישים מייל מקדיז ניצב בימי הביניים מבצר, שכל עקבותיו נעלמו במשך מאות שנים. בין שאר המאפיינים המעניינים, המבצר הזה הכיל צינוק לא נעים במיוחד, המחולק לשישה עשר תאים, כולם מתקשרים זה עם זה, כפי שמוצג באיור.

    עתה, המושל היה עליז, וחובב חידות גדול. יום אחד הוא הלך לצינוק ואמר לאסירים, "בחיי!" (או המקבילה שלו בספרדית) "כולכם תשוחררו אם תוכלו לפתור את החידה הזו. עליכם לסדר את עצמכם בשישה עשר התאים כך שהמספרים על גבכם יהוו ריבוע קסם שבו כל טור, כל שורה וכל אחד משני האלכסונים יסתכמו לאותו מספר. רק זכרו זאת: שאף אחד מכם לא יהיה ביחד באותו תא."

    אחד האסירים, לאחר שעבד על הבעיה במשך יומיים או שלושה, עם חתיכת גיר, לקח על עצמו להשיג את חירותו וחירות חבריו האסירים אם הם ילכו בעקבות הוראותיו ויעברו דרך הפתח מתא לתא בסדר שבו יקרא את המספרים שלהם. 

     

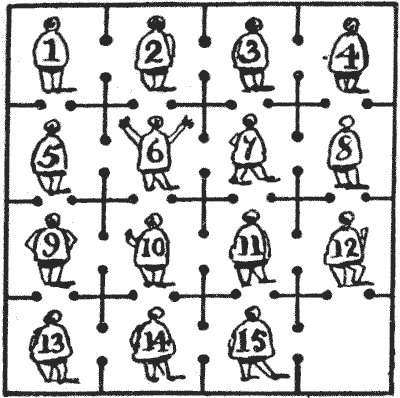
    הוא הצליח בניסיונו, ומה שמרשים יותר, כך נראה מהתיאור של שיטתו שנרשם בכתב היד העתיק שלפניי, שהוא עשה זאת במספר המהלכים המועט ביותר האפשרי. הקורא מתבקש להראות מה היו המהלכים האלה.

  • שאלה 404 - הצינוקים הסיביריים

     

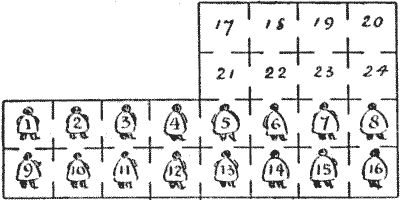
    למעלה מוצגת תוכנית מהימנה של בית כלא רוסי מסוים בסיביר. כל התאים ממוספרים, והאסירים ממוספרים במספרים זהים לתאים בהם הם נמצאים. תזונת הכלא כל כך משמינה שאסירים פוליטיים אלה חוששים תמידית שאם יגיע חנינה, הם לא יוכלו לדחוס את עצמם דרך הפתחים הצרים ולצאת. וכמובן שזה יהיה לא סביר לבקש מכל ממשלה להפיל את חומות הכלא רק כדי לשחרר את האסירים, יהיו אשר יהיו חפים מפשע. לכן אנשים אלה עושים את כל הפעילות הגופנית הבריאה שהם יכולים כדי לעכב את ההשמנה הגוברת שלהם, ואחד הבילויים שלהם ישמש אותנו כדי לספק את החידה הבאה.

    הראו, במספר המהלכים המועט ביותר האפשרי, כיצד ששת-עשר האסירים יכולים לסדר את עצמם בריבוע קסם, כך שהמספרים על גבם יסתכמו לאותו סכום בכל אחד מארבעת הטורים, ארבע השורות ושני האלכסונים, מבלי ששני אסירים היו אי פעם באותו תא יחד. מוטב שאומר, לידיעת אלה שעדיין לא הכירו את המקומות האלה, שאחת המוזרויות של בתי הכלא היא שלא מורשים לצאת מגבולות החומות שלהם. כל אסיר רשאי ללכת כל מרחק אפשרי במהלך בודד.

  • שאלה 405 - ריבועי קסם של קלפים

    קחו חפיסת קלפים רגילה והוציאו את שנים-עשר קלפי הפנים (נסיך, מלכה ומלך). כעת, עם תשעה מהקלפים הנותרים (הצבעים השונים אינם משנים), צרו את ריבוע הקסם שלמעלה. ניתן לראות שהערך המספרי של הקלפים מסתכם ל-`15` בכל שורה, בכל עמוד ובכל אחד משני האלכסונים הראשיים. החידה היא ליצור, בעזרת הקלפים הנותרים (מבלי לשנות את הסידור הזה), שלושה ריבועי קסם נוספים כאלה, כך שכל אחד מארבעת הריבועים יסתכם לסכום שונה. כמובן שיהיו ארבעה קלפים בחפיסה המצומצמת שלא ישמשו. ארבעת אלה יכולים להיות כל קלף שתבחרו. זו לא חידה קשה, אבל היא דורשת קצת מחשבה.

  • שאלה 406 - שמונה עשרה אבני דומינו

    האיור מציג שמונה עשרה אבני דומינו המסודרות בצורת ריבוע, כך שמספר הנקודות בכל אחד מששת הטורים, שש השורות ושני האלכסונים הארוכים מסתכם ל-`13`. זהו הסכום הקטן ביותר האפשרי עם מבחר כלשהו של אבני דומינו מקופסה רגילה של עשרים ושמונה. הסכום הגדול ביותר האפשרי הוא `23`, ופתרון למספר זה ניתן להשיג בקלות על ידי החלפת כל מספר במשלים שלו ל-`6`. לכן, עבור כל ריבוע ריק, החליפו `6`, עבור כל `1` החליפו `5`, עבור כל `2` החליפו `4`, עבור `3` החליפו `3`, עבור `4` החליפו `2`, עבור `5` החליפו `1`, ועבור `6` החליפו ריבוע ריק. אבל החידה היא לבצע בחירה של שמונה עשרה אבני דומינו ולסדר אותן (בדיוק בצורה המוצגת) כך שהסכומים יהיו `18` בכל ארבעה עשר הכיוונים שהוזכרו.

  • שאלה 407 - שְׁנֵי רִבּוּעִים קְסוּמִים חֲדָשִׁים

    בְּנוּ רִבּוּעַ קְסָם חִסּוּרִי עִם שִׁשָּׁה עָשָׂר הַמִּסְפָרִים הַשְּׁלֵמִים הָרִאשׁוֹנִים שֶׁיִּהְיוּ "מְקֻשָּׁרִים" עַל יְדֵי חִסּוּר. הַקּוֹנְסְטַנְטָה מֻשֶּׂגֶת, כַּמּוּבָן, עַל יְדֵי חִסּוּר הַמִּסְפָר הָרִאשׁוֹן מִן הַשֵּׁנִי בַּשּׁוּרָה, הַתּוֹצָאָה מִן הַשְּׁלִישִׁי, וְהַתּוֹצָאָה שׁוּב מִן הָרְבִיעִי. בְּנוּ גַּם רִבּוּעַ קְסָם חִלּוּקִי מֵאוֹתוֹ סֵדֶר שֶׁיִּהְיֶה "מְקֻשָּׁר" עַל יְדֵי חִלּוּק. הַקּוֹנְסְטַנְטָה מֻשֶּׂגֶת עַל יְדֵי חִלּוּק הַמִּסְפָר הַשֵּׁנִי בַּשּׁוּרָה בָּרִאשׁוֹן, הַשְּׁלִישִׁי בְּמָנֶה, וְהָרְבִיעִי בַּמָּנֶה הַבָּא.

  • שאלה 408 - ריבועי קסם מדרגה שנייה

    בזמן שקראתי חיבור מתמטי צרפתי, נתקלתי בהצהרה הבאה: "ריבוע קסם מדהים ביותר מסדר `8`, בשתי דרגות, נבנה על ידי מר פפרמן. במילים אחרות, הוא הצליח לסדר את שישים וארבעת המספרים הראשונים על משבצות לוח השחמט בצורה כזו שסכום המספרים בכל שורה, בכל טור ובכל אחד משני האלכסונים יהיה זהה; ויותר מכך, אם נחליף את כל המספרים בריבועים שלהם, הריבוע עדיין יישאר קסום." מיד ניגשתי לעבודה כדי לפתור את הבעיה הזו, ולמרות שהיא התבררה כאגוז קשה לפיצוח, זכיתי בגילוי של כמה חוקים מוזרים ויפים השולטים בה. ייתכן שהקורא ירצה לנסות את כוחו בפאזל.

  • שאלה 409 - סלי הפירות

     

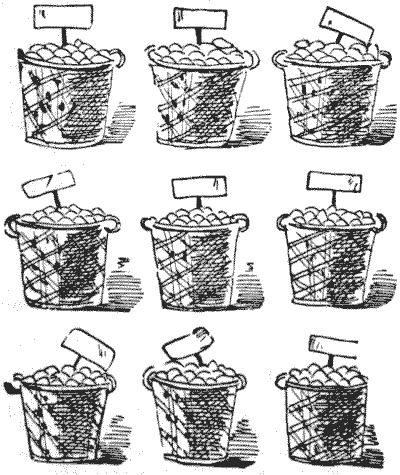
    זו הצורה שבה הצגתי לראשונה את השאלה של ריבועים קסומים עם מספרים ראשוניים. אני כאן מזהיר את הקורא שיש מלכודת קטנה.

    לסוחר פירות היו תשעה סלים. כל סל הכיל שזיפים (כולם שלמים ובשלים), והמספר בכל סל היה שונה. כאשר הם הוצבו כפי שמוצג באיור, הם יצרו ריבוע קסם, כך שאם הוא היה לוקח כל שלושה סלים בקו בשמונה הכיוונים האפשריים, תמיד יהיה אותו מספר של שזיפים. החלק הזה של הפאזל קל מספיק להבנה. אבל מה שבא לאחר מכן נראה ממבט ראשון קצת מוזר.

    הסוחר אמר לאחד מעובדיו לחלק את תכולת הסל שהוא יבחר בין כמה ילדים, ולתת שזיפים לכל ילד כך שכל אחד יקבל מספר שווה. אבל העובד גילה שזה בלתי אפשרי לחלוטין, לא משנה איזה סל הוא בחר ולא משנה כמה ילדים הוא כלל בפינוק. הראה, על ידי מתן תכולת תשעת הסלים, כיצד זה יכול לקרות.

  • שאלה 410 - החידה בצורת "T" של המנדרין

     

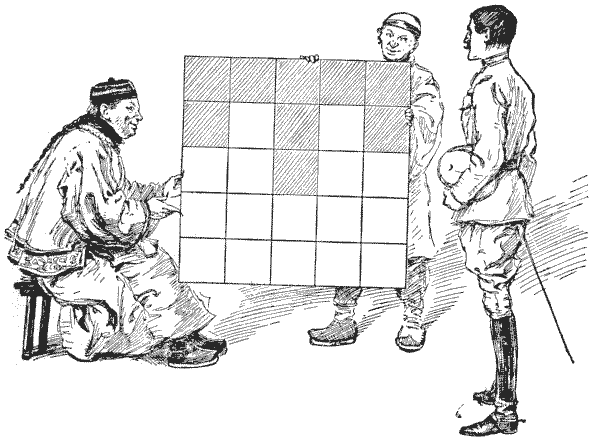
    לפני שמארג׳וריבנקס בושאמפ צ׳ולמונדלי יצא לסיורו במזרח הרחוק, הוא התגאה בידע שלו בריבועים קסומים, נושא שהפך לתחביב מיוחד שלו; אבל עד מהרה הוא גילה שמעולם לא נגע יותר מאשר בשולי הנושא, ושצ׳יני ערמומי יכול לנצח אותו בקלות. אני מציג בעיה קטנה שמנדרין מלומד הציג למטייל שלנו, כפי שמצויר בעמוד האחרון.

    הסיני, לאחר שהעיר שהבנייה של ריבוע קסם רגיל של עשרים וחמישה תאים היא "too velly muchee easy," ביקש מבן ארצנו למקם את המספרים `1` עד `25` בריבוע כך שכל עמודה, כל שורה וכל אחד משני האלכסונים יסתכמו ל-`65`, כאשר רק מספרים ראשוניים נמצאים על ה-"T" המוצלל. כמובן שהמספרים הראשוניים הזמינים הם `1, 2, 3, 5, 7, 11, 13, 17, 19`, ו-`23`, כך שיש לך חופש לבחור כל תשעה מהם שישרתו את מטרתך. האם אתה יכול לבנות את ריבוע הקסם הקטן והסקרן הזה?