תורת המספרים

תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.

מספרים ראשוניים משפט השאריות הסיני חשבון השאריות המחלק המשותף המקסימלי והכפולה המשותפת המינימלית מספרים משולשיים חלוקה

• מסגרת

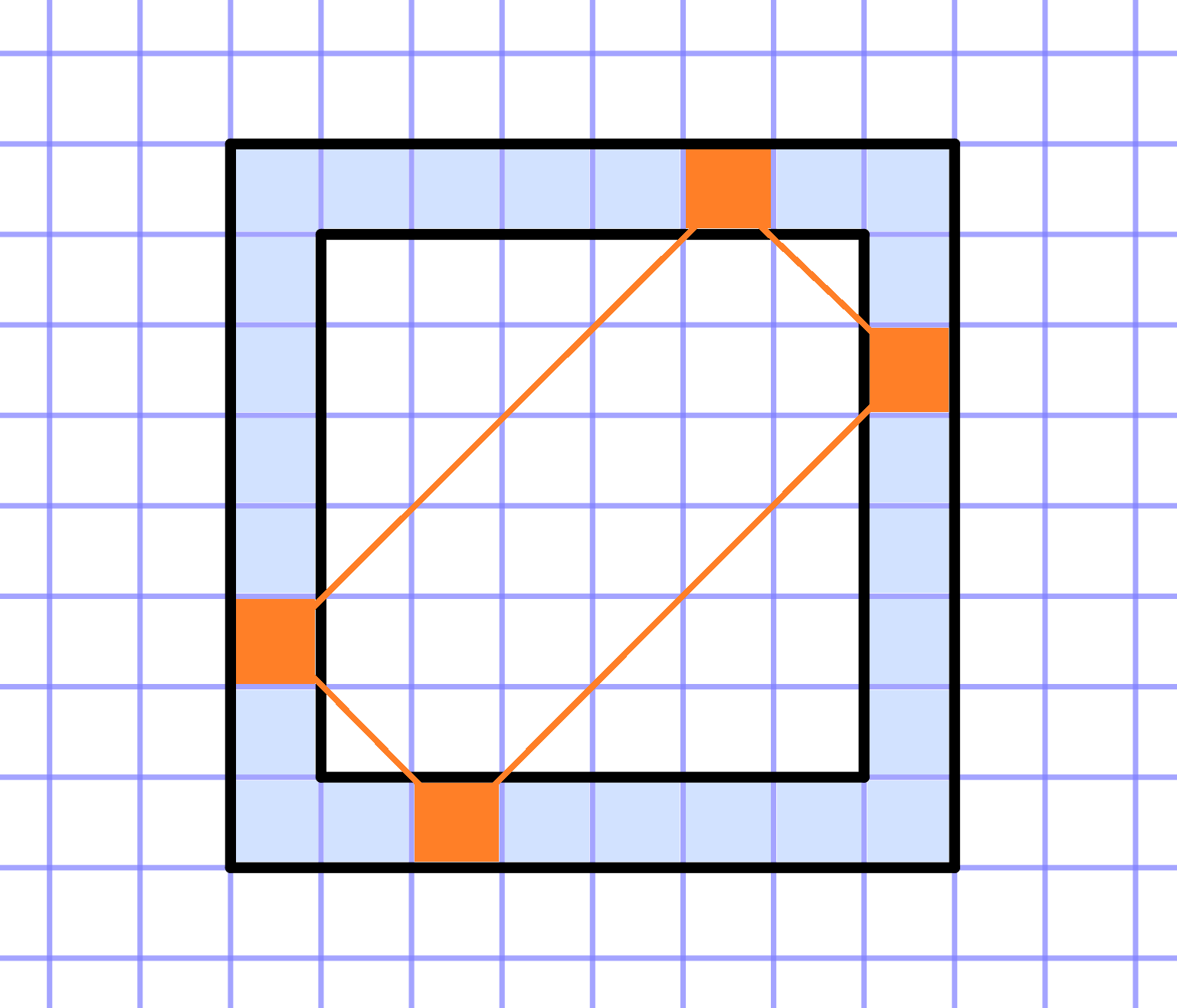
  על דף משבצות נתון ריבוע בגודל `NxxN`. נתבנן במסגרת שלו בעובי של משבצת אחת. היא מורכבת מ-`4*(N-1)` משבצות.

  האם תוכלו לרשום במשבצות של המסגרת `4*(N-1)` מספרים שלמים עוקבים (לא בהכרח חיוביים), כך שיתקיים התנאי הבא:

  לכל מלבן שקודקודיו נמצאים על המסגרת וצלעותיו מקבילים לאלכסונים של הריבוע המקורי, סכום המספרים בקודקודים שווה לגודל קבוע. זה כולל גם את המלבנים "המנוונים" בעלי רוחב אפס שמתלכדים עם האלכסונים של הריבוע - במקרה הזה פשוט סוכמים את שני המספרים בקודקודים המנוגדים של הריבוע

  עבור:

  א. `N=3`

  ב. `N=4`

  ג. `N=5`

  

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • תחרות הערים, תשמ"ד, סתיו, גרסת תרגול, כיתות ט-י שאלה 3 נקודות 2+3+4

• שאלה

  הוכיחו כי לא ניתן לחתוך את הצורה הנתונה לאבני דומינו:

  

  נושאים:

  קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> התאמות תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה קומבינטוריקה -> צביעות -> צביעת שחמט קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה

• שאלה

  כל אחד משבעה ילדים מחזיק ביד שני בלונים, אדום וצהוב. האם הם יכולים להתחלף בבלונים, כך שלכל אחד יהיו שני בלונים מאותו צבע?

  נושאים:

  לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות

• שאלה

  `19` עצי תפוחים ממוקמים במעגל. הוכיחו כי קיים זוג עצים סמוכים, שמספר התפוחים הכולל שיש עליהם הינו זוגי.

  נושאים:

  לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה

• שאלה

  בארץ הקסומה יש מטבעות של `4`, `7` ו-`10` לירות בלבד. לשלומי יש כרגע רק מטבעות של `4` ושל `10` לירות. ברצונו של שלומי לקנות ספר שעולה `23` לירות. האם הוא יצליח לשלם על הספר ללא עודף?

  נושאים:

  לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות

• שאלה

  האם תוכלו למצוא שני מספרים, שגם סכום, גם מכפלה שלהם אי זוגיים? נמקו או הביאו דוגמה!

  נושאים:

  תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה

• שאלה

  הוכיחו כי סכום של שני מספרים עוקבים תמיד אי זוגי.

  נושאים:

  תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה

• שאלה

  לאורך הרחוב ממוקמים `6` עצים. יום אחד הגיעו `6` תוכים והתיישבו על העצים, תוכי אחד על כל עץ. מידי פעם שני תוכים עוברים כל אחד לעץ סמוך לבחירתו. האם יוכלו התוכים להתכנס כולם על אותו עץ?

  נושאים:

  קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות

• בוחן

  בכיתה של 25 תלמידים התקיים בוחן המורכב מ-7 שאלות. הוכיחו כי לפחות אחד משני המשפטים הבאים נכון:

  1. יש ילד שפתר מספר אי זוגי של שאלות
  2. יש שאלה שפתרו אותה מספר זוגי של ילדים
  נושאים:

  קומבינטוריקה -> עקרון שובך היונים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> הוכחה בשלילה
  מקורות:
  • האולימפיאדה לצעירים, תשע"ח, גמר, כיתות ה-ו שאלה 5

• מעגל שקרנים - טענת האמת

  במעגל יושבים n אנשים, כל אחד מהם הוא שקרן או דובר אמת.

  האנשים מסתכלים למרכז המעגל. שקרן תמיד משקר, ודובר אמת תמיד אומר אמת.

  כל אחד מהאנשים יודע בדיוק מי דובר שקר ומי דובר אמת.

  כל אחד מהאנשים אומר שהאיש שיושב שני מקומות לשמאלו (זאת אומרת ליד האיש שיושב לידו), הוא דובר אמת.

  ידוע שבמעגל יש לפחות שקרן אחד, ולפחות דובר אמת אחד.

  א. האם ייתכן ש-2017 = n?

  ב. האם ייתכן ש-5778 = n?

  (פורמט פתרון: "מילה, מילה" למשל "חתול, כלבלב")

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים הוכחה ודוגמה -> הוכחה בשלילה לוגיקה -> דוברי אמת ושקרנים
  מקורות:
  • אולימפיאדת גיליס, תשע"ח שאלה 1