תורת המספרים

תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.

מספרים ראשוניים משפט השאריות הסיני חשבון השאריות המחלק המשותף המקסימלי והכפולה המשותפת המינימלית מספרים משולשיים חלוקה

• ארבעה מספרים

  נתונים ארבעה מספרים שלמים חיוביים שונים. סכום המספרים האלה שווה ל-18.
  בנוסף, ידוע שהמכפלה של ארבעת המספרים האלה אי זוגית. חשבו את המכפלה הזאת

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה -> זוגיות
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, שלב א, כיתות ג-ד שאלה 4

• חמישה מספרים

  נתונים חמישה מספרים שלמים חיובים שונים. סכום המספרים האלה שווה ל-27. בנוסף, ידוע שהמכפלה של חמשת המספרים האלו הינה אי זוגית. חשבו את המכפלה הזו.

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה -> זוגיות
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, שלב א, כיתות ה-ו שאלה 4

• מקדמים שלמים?

  נתונים מספרים ממשיים a,b,c כך שעבור כל מספר שלם x המספר `ax^2+bx+c` שלם. האם זה בהכרח אומר ש a,b,c כולם שלמים? הוכיחו שכן או הביאו דוגמא נגדית.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  אלגברה תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> בניית דוגמה
  מקורות:
  • תחרות גרוסמן, 2017, צעירים שאלה 2

• שיוויון בשלבים

  על הלוח כתובים המספרים 1,2,3,4,5,6,7,8,9,10 ודוד אמור לשנות אותם בשלבים. בכל שלב מותר לדוד לבחור שני מספריים ולשנות אותם ב 1, כלומר להוסיף לשניהם 1, להחסיר משניהם 1, או להוסיף לאחד 1 ולהחסיר מהשני 1.

  האם דוד יוכל אחרי מספר שלבים להגיע למצב שבו כל המספרים על הלוח שווים? אם כן תראו דוגמא ואם לא נמקו את תשובתכם בפירוט.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • תחרות גרוסמן, 2017, צעירים שאלה 3

• שניים רבים השלישי לוקח

  השכבה כולה במחלוקת!

  42 חושבים ש-כן, 43 חושבים ש-אולי ו-36 חושבים ש-לא.

  כאשר שניים שחושבים אחרת זה מזה נפגשים - שניהם משנים את עמדתם לזו השלישית.

  כמה מפגשים לכל הפחות צריכים להתקיים עד שכולם יסכימו על אותה העמדה?

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • תחרות החידמטיקה השבועית של בר אילן, 2024 שאלה 9

• שאלה

  במעגל נמצאות 5778 נורות כבויות במרחקים קבועים. מתחת לכל נורה יש כפתור. כאשר לוחצים על הכפתור, זה משנה מצב של 4 נורות: הנורה שליד הכפתור, שתי נורות הבאות במעגל עם כיוון השעון, ואת הנורה הנגדית לכפתור (נורה כבויה נדלקת כאשר משנים את מצבה, ונורה דולקת נכבית). מהי הכמות המרבית של נורות שיכולות להיות דלוקות בו-זמנית?
  

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> אינווריאנטים לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> צביעות
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 8

• טבעות הברזל המייגעות

   

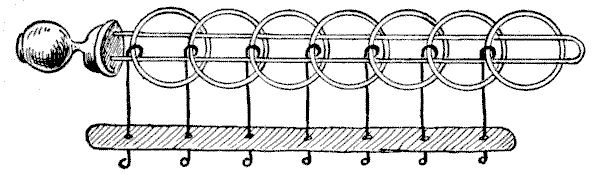
  האיור מייצג אחד מהחידות המכאניות העתיקות ביותר. מקורו אינו ידוע. קרדנו, המתמטיקאי, כתב עליו בשנת `1550`, וואליס בשנת `1693`; בעוד שאומרים שהוא עדיין נמצא בכפרים אנגליים נידחים (לפעמים מונח במקומות מוזרים, כמו מגדל פעמונים של כנסייה), עשוי מברזל, ונקרא באופן הולם "טבעות מייגעות", ומשמש את הנורווגים כיום כמנעול לקופסאות ותיקים. בחנויות הצעצועים הוא נקרא לפעמים "טבעות סיניות", אם כי נראה שאין סמכות לתיאור, ולרוב הוא מכונה בשם הלא מספק "הטבעות המבלבלות". הצרפתים קוראים לזה "Baguenaudier."

  ניתן לראות שהחידה מורכבת מ-לולאה פשוטה של חוט המקובעת בידית שאותה מחזיקים ביד שמאל, וממספר מסוים של טבעות המאובטחות על ידי חוטים העוברים דרך חורים ב-מוט ונשמרים שם על ידי קצותיהם הקהים. החוטים פועלים בחופשיות במוט, אך אינם יכולים להיפרד ממנו, וגם לא ניתן להסיר את החוטים מהטבעות. החידה הכללית היא לנתק את הלולאה לחלוטין מכל הטבעות, ואז להחזיר את כולן שוב.

  כעת, ניתן לראות במבט חטוף שניתן להסיר את הטבעת הראשונה (מימין) בכל עת על ידי החלקתה מעל הקצה והשלכתה דרך הלולאה; או שאפשר להחזיר אותה על ידי היפוך הפעולה. מלבד זאת, הטבעת היחידה שניתן להסיר אי פעם היא זו שבמקרה נמצאת השנייה הסמוכה על הלולאה בקצה הימני. כך, כשכל הטבעות עליה, ניתן להפיל את השנייה מיד; כשהטבעת הראשונה למטה, אינך יכול להפיל את השנייה, אך תוכל להסיר את השלישית; כששלוש הטבעות הראשונות למטה, אינך יכול להפיל את הרביעית, אך תוכל להסיר את החמישית; וכן הלאה. יתברר שאפשר להפיל את הטבעות הראשונה והשנייה יחד או להחזיר אותן יחד; אך כדי למנוע בלבול, לא נאפשר את המהלך הכפול החריג הזה, ונגיד שניתן להחזיר או להסיר רק טבעת אחת בכל פעם.

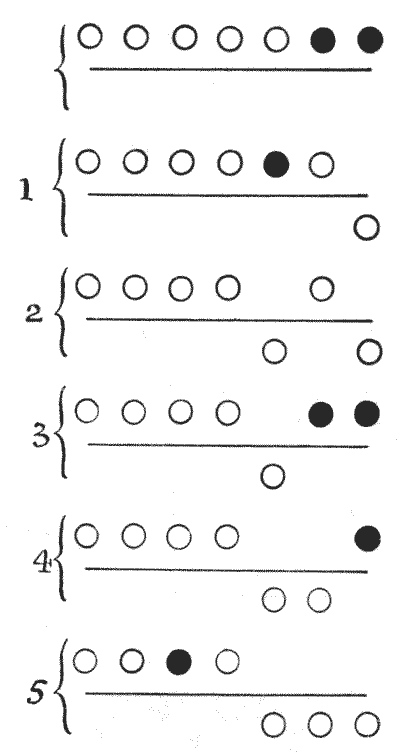
  אנו יכולים להסיר טבעת אחת ב-`1` מהלך; שתי טבעות ב-`2` מהלכים; שלוש טבעות ב-`5` מהלכים; ארבע טבעות ב-`10` מהלכים; חמש טבעות ב-`21` מהלכים; ואם נמשיך להכפיל (ולהוסיף אחד כאשר מספר הטבעות הוא אי-זוגי) נוכל לברר בקלות את מספר המהלכים להסרת כל מספר טבעות לחלוטין. כדי להוריד את כל שבע הטבעות נדרשים `85` מהלכים. בואו נסתכל על חמשת המהלכים שנעשו בהסרת שלוש הטבעות הראשונות, העיגולים מעל הקו מייצגים טבעות על הלולאה ואלה שמתחת מייצגים טבעות מחוץ ללולאה.

  הפילו את הטבעת הראשונה; הפילו את השלישית; הרימו את הראשונה; הפילו את השנייה; והפילו את הראשונה—`5` מהלכים, כפי שמוצג בבירור בתרשימים. העיגולים הכהים מראים בכל שלב, ממצב ההתחלה ועד הסיום, אילו טבעות אפשר להפיל. לאחר מהלך `2` יורגש שלא ניתן להפיל אף טבעת עד שאחת תוחזר, מכיוון שהטבעות הראשונה והשנייה מימין שנמצאות כעת על הלולאה אינן יחד. לאחר המהלך החמישי, אם ברצוננו להסיר את כל שבע הטבעות, עלינו כעת להפיל את החמישית. אבל לפני שנוכל להסיר אז את הרביעית, יש צורך להחזיר את שלוש הראשונות ולהסיר את שתי הראשונות. אז יהיו לנו `7, 6, 4, 3` על הלולאה, ולכן נוכל להפיל את הרביעית. כשנחזיר `2` ו-`1` ונסיר `3, 2, 1`, נוכל להפיל את הטבעת השביעית. הפעולה הבאה אז תהיה להשיג `6, 5, 4, 3, 2, 1` על הלולאה ולהסיר `4, 3, 2, 1`, ואז `6` תרד; ואז להשיג `5, 4, 3, 2, 1` על הלולאה, ולהסיר `3, 2, 1`, ואז `5` תרד; ואז להשיג `4, 3, 2, 1` על הלולאה ולהסיר `2, 1`, ואז `4` תרד; ואז להשיג `3, 2, 1` על הלולאה ולהסיר `1`, ואז `3` תרד; ואז להשיג `2, 1` על הלולאה, ואז `2` תרד; ו-`1` תיפול דרך במהלך ה-85, ותשאיר את הלולאה חופשית לחלוטין. על הקורא להיות מסוגל כעת להבין את החידה, בין אם יש לו אותה ביד בצורה מעשית ובין אם לא.

   

  הבעיה המסוימת שאני מציע היא פשוט זו. נניח שיש בסך הכל ארבע עשרה טבעות על טבעות הברזל המייגעות, ואנו ממשיכים להסיר את כולן בצורה הנכונה כדי לא לבזבז אף מהלך. מה יהיה מצב הטבעות לאחר שבוצע המהלך ה-`9`,999?

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה -> זוגיות אלגברה -> סדרות -> נוסחאות נסיגה קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 417

• שאלה

  בחדר יש כיסאות עם `4` רגליים ועם `3` רגליים. כאשר על כל הכיסאות התיישבו אנשים, נהיה `39` רגליים בחדר (לא נשארו אנשים שעומדים). כמה כיסאות מכל סוג יש בחדר?

  נושאים:

  אלגברה -> בעיות מילוליות תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית -> אלגוריתם אוקלידס אלגברה -> משוואות -> משוואות דיופנטיות

• שאלה

  בארץ הקסומה יש רק שני סוגים של מטבעות: `16` ל"ק (לירות קסומות) ו-`27` ל"ק. האם ניתן לקנות מחברת שעולה לירה קסומה אחת ולקבל עודף מדויק?

  נושאים:

  הוכחה ודוגמה -> בניית דוגמה תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית -> אלגוריתם אוקלידס תורת המספרים -> חלוקה אלגברה -> משוואות -> משוואות דיופנטיות

• חילוק פשוט

  לפעמים שאלה פשוטה מאוד באריתמטיקה אלמנטרית תגרום למבוכה רבה. לדוגמה, אני רוצה לחלק את ארבעת המספרים, `701, 1,059, 1,417`, ו-`2,312`, במספר הגדול ביותר האפשרי שישאיר את אותה שארית בכל מקרה. איך אני אמור להתחיל לעבוד? כמובן, על ידי מערכת ניסויים מייגעת אפשר עם הזמן לגלות את התשובה, אבל יש שיטה די פשוטה לעשות זאת אם רק תוכל למצוא אותה.
  נושאים:

  אריתמטיקה תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית -> אלגוריתם אוקלידס תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 127