תורת המספרים

תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.

• הספרות שהתחפשו

  בתרגיל החילוק שלפניכם, (כמעט) כל הספרות התחפשו!

  מהו המספר המחולק?

  \(\begin{align*} &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }**\text{ }8**\\ &\overline{* * * * * * *\text{ } *}| * *\text{ } *\\ &\underline{\text{ }\text{ }* *\text{ } *}\\ &\text{ }\text{ }\text{ }\text{ }\text{ }* * * *\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\underline{\text{ }\text{ }* *\text{ } *}\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }* * * *\\ &\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\underline{* * *\text{ } *}\\ \end{align*}\)

  נושאים:

  אריתמטיקה תורת המספרים -> חלוקה חידות ורבוסים -> שחזרו את התרגיל
  מקורות:
  • תחרות החידמטיקה השבועית של בר אילן, 2024 שאלה 8

• שק האגוזים

  לשלושה בנים ניתנה שקית אגוזים כמתנת חג המולד, והוסכם שהם יחולקו ביחס לגילם, שביחד הסתכם ל-`17 1/2` שנים. עכשיו השק הכיל `770` אגוזים, וכאשר הרברט לקח ארבעה, רוברט לקח שלושה, וכאשר הרברט לקח שישה, כריסטופר לקח שבעה. החידה היא לגלות כמה אגוזים היו לכל אחד, ומה היו הגילאים של הבנים.

  נושאים:

  אלגברה -> בעיות מילוליות אריתמטיקה -> שברים אלגברה -> אי שוויונים -> ממוצעים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 50

• תעלומת רציף ופשו

  הייתה מהומה גדולה ברחוב תמזה התחתון בבוקר ה-`12` בינואר `1887`. כאשר חברי הצוות המוקדמים הגיעו לרציף ופשו, הם גילו שהכספת נפרצה, סכום כסף ניכר נלקח והמשרדים היו במצב של אי סדר גדול. השומר הלילי לא היה בשום מקום, אבל אף אחד שהכיר אותו לרגע לא חשד בו שהוא אשם בשוד. באמונה זו אושרה דעתם של הבעלים כאשר, מאוחר יותר באותו יום, הם קיבלו הודעה שגופתו של המסכן נמצאה על ידי משטרת הנהר. סימני אלימות מסוימים הצביעו על העובדה שהוא הותקף באכזריות והושלך לנהר. שעון שנמצא בכיסו נעצר, כפי שקורה תמיד בנסיבות כאלה, וזה היה רמז רב ערך לשעת הפשע. אבל קצין טיפש מאוד (ואנחנו תמיד מוצאים אינדיבידואלים טיפשים אחד או שניים בגופים האינטליגנטיים ביותר של אנשים) למעשה שעשע את עצמו על ידי סיבוב המחוגים שוב ושוב, מנסה להפעיל את השעון שוב. לאחר שננזף בחריפות על שיקול הדעת החמור הזה, הוא נשאל אם הוא זוכר את השעה שהוצגה על ידי השעון כשנמצא. הוא השיב שהוא לא זוכר, אבל הוא נזכר שמחוג השעות ומחוג הדקות היו בדיוק ביחד, אחד מעל השני, ומחוג השניות בדיוק עבר את השנייה הארבעים ותשע. יותר מזה הוא לא זכר.

  מה הייתה השעה המדויקת שבה נעצר השעון של השומר? מניחים כמובן שהשעון היה מדויק.

  נושאים:

  לוגיקה -> הגיון אריתמטיקה -> שברים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 60

• עשרת המונים

  במקרה זה אנו משתמשים באפס בנוסף ל-`1, 2, 3, 4, 5, 6, 7, 8, 9`. החידה היא, כבמקרה הקודם, לסדר את עשרת המונים כך שמכפלות שני הכפל יהיו זהות, ואפשר שיהיו ספרה אחת או יותר במכפיל, כרצונך. האמור לעיל הוא הישג קל מאוד; אך נדרש גם למצוא את שני הסידורים הנותנים זוגות של המכפלות הגבוהות והנמוכות ביותר האפשריות. כמובן שיש להשתמש בכל מונה, ולא ניתן למקם את הספרה אפס משמאל לשורת ספרות כאשר אין לה השפעה. שברים פשוטים או עשרוניים אינם מותרים.
  נושאים:

  אריתמטיקה קומבינטוריקה -> בדיקת מקרים -> תהליכים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 82

• ארבע פעמים שבע

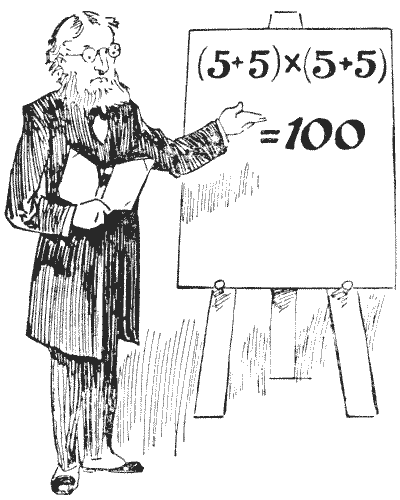  באיור נראה פרופסור ראקבריין מדגים אחד מהתחבולות הקטנות שבהן הוא רגיל לבדר את הכיתה שלו. הוא מאמין שעל ידי הוצאת תלמידיו ממסלולים שחוקים הוא מסוגל יותר להבטיח את תשומת ליבם, ולגרום לשיטות חשיבה מקוריות ומתוחכמות. כפי שנראה, הוא בדיוק הראה כיצד ניתן לכתוב ארבע פעמים `5` עם סימנים אריתמטיים פשוטים כך שיצייגו `100`. כל קורא צעיר יראה במבט חטוף שהדוגמה שלו נכונה לחלוטין. עכשיו, מה שהוא רוצה שתעשו זה: סדרו ארבע פעמים `7` (לא יותר ולא פחות) עם סימנים אריתמטיים כך שהם ייצגו `100`. אם הוא היה אומר שעלינו להשתמש בארבע פעמים `9`, מיד היינו יכולים לכתוב `99 9/9`, אבל ארבע פעמים `7` דורשות קצת יותר תושייה. האם תוכלו לגלות את הטריק הקטן?

  נושאים:

  אלגברה -> משוואות אריתמטיקה -> שברים תורת המספרים -> חלוקה חידות ורבוסים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 95

• מורשת מבלבלת

  אדם הוריש מאה דונם אדמה לחלוקה בין שלושת בניו - אלפרד, בנימין וצ'ארלס - ביחס של שליש, רבע וחמישית בהתאמה. אבל צ'ארלס נפטר. איך יש לחלק את האדמה בצורה הוגנת בין אלפרד ובנימין?
  נושאים:

  אלגברה -> בעיות מילוליות אריתמטיקה -> שברים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 112

• חידת מעונות

  במנזר מסוים היו שמונה מעונות גדולים בקומה אחת, שאליהם הגיעה גרם מדרגות ספירלי במרכז, כפי שמוצג בתרשים שלנו. בבדיקה שערכה אם המנזר ביום שני אחד, התגלה שהצד הדרומי מועדף כל כך, שפי שישה נזירות ישנו בצד הדרומי מאשר בכל אחד משלושת הצדדים האחרים. היא התנגדה לצפיפות היתר הזו, והורתה לצמצם אותה. ביום שלישי היא גילתה שפי חמש נזירות ישנו בצד הדרומי מאשר בכל אחד מהצדדים האחרים. שוב היא התלוננה. ביום רביעי היא מצאה פי ארבעה בצד הדרומי, ביום חמישי פי שלושה, וביום שישי פי שניים. לאחר שהאיצה בנזירות להמשיך במאמצים, היא שמחה לגלות ביום שבת שמספר שווה ישן בכל אחד מארבעת צדי הבית. מהו המספר הקטן ביותר של נזירות שיכול היה להיות שם, וכיצד הן יכלו להסתדר בכל אחד מששת הלילות? אסור שאף חדר יהיה ריק.

  
  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות תורת המספרים -> חלוקה
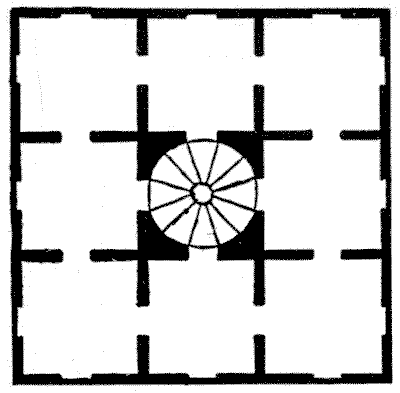  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 278

• חביות הדבש

   

  לפני זמן רב היה סוחר קשיש מבגדד שהיה מכובד מאוד על ידי כל מי שהכיר אותו. היו לו שלושה בנים, והיה לו כלל בחיים להתייחס לכולם בדיוק אותו הדבר. בכל פעם שאחד קיבל מתנה, שני האחרים קיבלו כל אחד מתנה בשווי שווה. יום אחד האיש הראוי הזה חלה ומת, והוריש את כל רכושו לשלושת בניו בחלקים שווים.

  הקושי היחיד שהתעורר היה בנוגע למלאי הדבש. היו בדיוק עשרים ואחת חביות. הזקן השאיר הוראות שלא רק שכל בן יקבל כמות שווה של דבש, אלא יקבל בדיוק את אותו מספר חביות, ושאף דבש לא יועבר מחבית לחבית בגלל הבזבוז הכרוך בכך. כעת, מכיוון ששבע מהחביות הללו היו מלאות בדבש, שבע היו חצי מלאות ושבע היו ריקות, התברר שזה די פאזל, במיוחד כאשר כל אח התנגד לקחת יותר מארבע חביות מאותו תיאור—מלאות, חצי מלאות או ריקות. האם אתה יכול להראות כיצד הם הצליחו לבצע חלוקה נכונה של הרכוש?

  נושאים:

  אלגברה -> בעיות מילוליות אריתמטיקה -> שברים קומבינטוריקה -> בדיקת מקרים -> תהליכים תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 372

• שאלה

  `120` כדורים זהים מונחים בצורה של פירמידה משולשת. כמה שכבות יש בפירמידה?

  הערה: מדובר בפירמידה, שהיא צורה תלת מימדית, ולא במשולש במישור.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במרחב אריתמטיקה לוגיקה -> הגיון הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית אלגברה -> סדרות -> השלימו\המשיכו סדרה תורת המספרים -> מספרים משולשיים

• מחקר בחיסכון

  מספרים מסוימים נקראים משולשים, משום שאם הם מייצגים סופרים או מטבעות, ניתן לסדר אותם על השולחן בצורה של משולשים. המספר `1` תמיד נחשב למשולש, בדיוק כפי ש-`1` הוא מספר ריבועי ומספר מעוקב. הניחו מונה אחד על השולחן — זהו המספר המשולשי הראשון. כעת הניחו שני מונים נוספים מתחתיו, ויש לכם משולש של שלושה מונים; לכן `3` הוא משולשי. לאחר מכן הניחו שורה של שלושה מונים נוספים, ויש לכם משולש של שישה מונים; לכן `6` הוא משולשי. אנו רואים שכל שורת מונים שאנו מוסיפים, המכילה מונה אחד יותר מהשורה שמעליה, יוצרת משולש גדול יותר.

  כעת, מחצית מסכום של כל מספר והריבוע שלו היא תמיד מספר משולשי. כך, מחצית מ-`2` + `2`^`2` = `3`; מחצית מ-`3` + `3`^`2` = `6`; מחצית מ-`4 + 4`^`2` = `10`; מחצית מ-`5` + `5`^`2`= `15`; וכן הלאה. אז אם אנו רוצים ליצור משולש עם `8` מונים בכל צד, נצטרך מחצית מ-`8 + 8`^`2`, או `36` מונים. זוהי תכונה קטנה ויפה של מספרים. לפני שאמשיך הלאה, אני אומר כאן שאם הקורא יעיין ב"בעיית הבנאי" (מס' `135`), הוא יזכור שסכום כל מספר של קוביות עוקבות המתחילות ב-`1` הוא תמיד ריבוע, ואלה יוצרים את הסדרה `1`^`2`, `3`^`2`, `6`^`2`, `10`^`2` וכו'. כעת יובן כאשר אני אומר שאחד המפתחות לחידה היה העובדה שאלה הם תמיד הריבועים של מספרים משולשים—כלומר, הריבועים של `1, 3, 6, 10, 15, 21, 28` וכו', כל אחד מהמספרים האלה, כפי שראינו, ייצור משולש.

  כל מספר שלם הוא או משולשי, או סכום של שני מספרים משולשים, או סכום של שלושה מספרים משולשים. כלומר, אם ניקח כל מספר שנבחר, תמיד נוכל ליצור משולש אחד, שניים או שלושה משולשים איתם. המספר `1` באופן ברור, ובאופן ייחודי, ייצור רק משולש אחד; מספרים מסוימים ייצרו רק שני משולשים (כמו `2, 4, 11` וכו'); מספרים מסוימים ייצרו רק שלושה משולשים (כמו `5, 8, 14` וכו'). אז, שוב, מספרים מסוימים ייצרו גם משולש אחד וגם שניים (כמו `6`), אחרים גם משולש אחד וגם שלושה (כמו `3` ו-`10`), אחרים גם שניים וגם שלושה משולשים (כמו `7` ו-`9`), בעוד שמספרים מסוימים (כמו `21`) ייצרו משולש אחד, שניים או שלושה, כרצוננו. כעת לחידה קטנה במספרים משולשים.

  סנדי מקאליסטר, מאברדין, נהג במשק בית קפדני, והיה להוט לאמן את אשתו הטובה בהרגלי החיסכון שלו. הוא אמר לה בערב השנה החדשה האחרון שכאשר היא תחסוך כל כך הרבה מטבעות זהב שהיא תוכל לפרוס את כולם על השולחן כדי ליצור ריבוע מושלם, או משולש מושלם, או שני משולשים, או שלושה משולשים, בדיוק כפי שהוא עשוי לבחור לבקש, הוא יוסיף חמישה פאונד לאוצר שלה. עד מהרה היא הלכה לבעלה עם שקית קטנה של £`36` במטבעות זהב ודרשה את הפרס שלה. יתברר ששלושים וששת המטבעות ייצרו ריבוע (עם צלע `6`), שהם ייצרו משולש בודד (עם צלע `8`), שהם ייצרו שני משולשים (עם צלעות `5` ו-`6`), ושהם ייצרו שלושה משולשים (עם צלעות `3, 5` ו-`5`). בכל אחד מארבעת המקרים כל שלושים וששת המטבעות משמשים, כנדרש, ולכן סנדי העניק לאשתו את המתנה שהובטחה כמו איש ישר.

  הסקוטי לאחר מכן התחייב להאריך את הבטחתו לחמש שנים נוספות, כך שאם בשנה הבאה מספר מטבעות הזהב המוגדל שהיא חסכה יוכל להיפרס בארבע הדרכים השונות, היא תקבל מתנה שנייה; אם היא תצליח בשנה שלאחר מכן היא תקבל מתנה שלישית, וכן הלאה עד שהיא תרוויח שש מתנות בסך הכל. עכשיו, כמה מטבעות זהב היא צריכה לשים ביחד לפני שהיא תוכל לזכות במתנה השישית?

  מה שאתם צריכים לעשות הוא למצוא חמישה מספרים, הקטנים ביותר האפשריים, הגבוהים מ-`36`, שניתן להציג בארבע הדרכים—ליצור ריבוע, ליצור משולש, ליצור שני משולשים, וליצור שלושה משולשים. הגבוה מבין חמשת המספרים שלכם יהיה התשובה שלכם.

  נושאים:

  תורת המספרים -> מספרים משולשיים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 137