תורת המספרים

תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.

• שאלה

  נתון מספר טבעי `n` שגדול מסכום ספרותיו פי שלוש. הוכיחו כי `n` מתחלק ב-`27`.

  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 הוכחה ודוגמה

• שאלה

  יהי `n` מספר טבעי. הוכיחו כי אם סכום ספרותיו של `5n` שווה לסכום ספרותיו של `n`, אז `n` מתחלק ב-`9`.

  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9

• מספר פלינדרומי

  מצאו מספר ארבע ספרתי פלינדרומי, שמתחלק ב-25 ולא מתחלק ב-3

  הערה: מספר פלינדרומי הינו מספר שלא ישתנה אם נקרא את הספרות שלו בסדר הפוך. למשל, המספר 5775 הינו מספר פלינדרומי, והמספר 5778 אינו מספר פלינדרומי.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 תורת המספרים -> חלוקה -> זוגיות תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-5 וב-25 קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • האולימפיאדה לצעירים, תשע"ח, שלב א, כיתות ג-ד שאלה 5

• 50 בחזקת

  הראו כי ב504 הספרות הימניות של `1+50+50^2+...+50^1000`

  מופיעה כל ספרה בכמות שמתחלקת ב 12 פעמים

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 אלגברה -> סדרות -> סדרה חשבונית אלגברה -> טכניקה אלגברית -> סכומים טלסקופיים
  מקורות:
  • תרגילי מינק וחומרים נוספים מאתר תחרות, תשע"ט, תרגיל 3 שאלה 2

• עוד 2 או 5 אבל לא 3

  כמה מספרים חמש ספרתיים מתחלקים ב-2 או ב-5, ולא מתחלקים ב-3?

  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 קומבינטוריקה -> כלל המכפלה
  מקורות:
  • האולימפיאדה לצעירים, תשע"ט, שלב ב, כיתות ה-ו שאלה 4

• 6 על הלוח

  על הלוח כתוב המספר 6. בכל שלב מותר להוסיף את הספרה 6 לסוף המספר (כך שהיא תהיה ספרת האחדות,) או להחליף את המספר בסכום הספרות שלו.
  אילו מספרים ניתן לקבל בדרך זו? יש לתאר את כל קבוצת המספרים ולהסביר למה אין יותר

  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 קומבינטוריקה -> אינדוקציה לוגיקה -> הגיון תורת המספרים -> חלוקה -> זוגיות אלגברה -> סדרות קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • האולימפיאדה לצעירים, תשע"ט, גמר, כיתות ג-ד שאלה 6
  • האולימפיאדה לצעירים, תשע"ט, גמר, כיתות ה-ו שאלה 5

• כרטיסים עם ספרות

  לרחל יש שלושה כרטיסים עם ספרות שונות, שכולן גדולות מ-0. רחל הרכיבה מהכרטיסים האלה את כל המספרים התלת ספרתיים האפשריים וחישבה את סכומם.
  הוכיחו כי הסכום מתחלק ב-3

  נושאים:

  תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 לוגיקה -> הגיון הוכחה ודוגמה
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ג-ד שאלה 6
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ה-ו שאלה 5

• שאלה

  על הלוח כתובים כל המספרים מ-1 עד `10^9` (כולל `10^9`). המספרים שמתחלקים ב-3 כתובים באדום, ושאר המספרים בכחול. סכום של כל המספרים האדומים שווה ל- `X`, וסכום של כל המספרים הכחולים שווה ל- `Y`. איזה מספר גדול יותר, `2X` או `Y`, ובכמה?

  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 לוגיקה -> הגיון אלגברה -> סדרות אלגברה -> אי שוויונים -> ממוצעים תורת המספרים -> חלוקה
  מקורות:
  • אולימפיאדת בנו ארבל, 2017, כיתה ח שאלה 2

• חבית הבירה

  אדם קנה כמות מוזרה של יין בחביות וחבית אחת המכילה בירה. אלה מוצגים באיור, המסומנים במספר הגלונים שכל חבית הכילה. הוא מכר כמות מהיין לאדם אחד וכמות כפולה לאחר, אך שמר את הבירה לעצמו. החידה היא לציין איזו חבית מכילה בירה. האם אתה יכול לומר איזו מהן זו? כמובן, האיש מכר את החביות בדיוק כפי שקנה אותן, מבלי לתפעל בשום צורה את התכולה.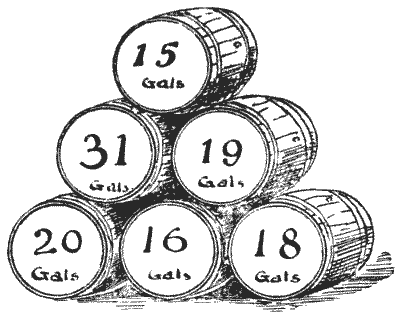
  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 אלגברה -> בעיות מילוליות לוגיקה -> הגיון
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 76

• חילוק דיגיטלי

  זוהי חידה טובה נוספת לסדר את תשע הספרות (ללא הספרה אפס) לשתי קבוצות כך שקבוצה אחת, כאשר מחלקים אותה בשנייה, תניב מספר נתון ללא שארית. לדוגמה, `1` `3` `4` `5` `8` חלקי `6` `7` `2` `9` נותן `2`. האם הקורא יכול למצוא סידורים דומים המניבים `3, 4, 5, 6, 7, 8` ו-`9` בהתאמה? כמו כן, האם הוא יכול למצוא את זוגות המספרים הקטנים ביותר האפשריים בכל מקרה? לדוגמה, `1` `4` `6` `5` `8` חלקי `7` `3` `2` `9` נכון באותה מידה עבור `2` כמו הדוגמה האחרת שנתנו, אך המספרים גבוהים יותר.
  נושאים:

  אריתמטיקה תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 תורת המספרים -> חלוקה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 88