גאומטריה, גאומטריה במישור

גאומטריה במישור עוסקת בצורות וגופים על משטח שטוח ודו-ממדי. היא מכסה תכונות של נקודות, קווים, זוויות, מצולעים (כמו משולשים ומרובעים) ומעגלים. שאלות כוללות בדרך כלל הוכחות, בנייה וחישובים הקשורים לאלמנטים אלו.

חשבון שטחים משולשים מעגלים סימטריה חשבון זוויות משפט פיתגורס אי שוויון המשולש

• 5 ישרים, 8 חיתוכים

  ציירו 5 ישרים, כך שתהיינה ביניהם בדיוק 8 נקודות חיתוך.

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ג-ד שאלה 1

• כחול או כתום?

  בציור ריבוע ABCD ומקבילית BCEF. איזה שטח גדול יותר: הכחול או הכתום?

  

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ה-ו שאלה 3

• השביל הכתום

  בציור מסביב לריבוע הכחול יש שביל כתום. השטח של השביל הוא 44% מהשטח של הריבוע.
  מהו הרוחב של השביל הכתום באחוזים יחסית לאורך הצלע של הריבוע הכחול?

  

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים אלגברה -> בעיות מילוליות אריתמטיקה -> אחוזים
  מקורות:
  • האולימפיאדה לצעירים, תשפ"א, שלב א, כיתות ה-ו שאלה 3

• מגן דוד במעגל

  על מעגל נתונות 8 נקודות. בכמה דרכים שונות אפשר לצייר מגן דוד עם קודקודים בנקודות האלו?

  

  הערה: מגן דוד הינה צורה כשמתקבלת כאשר שני משולשים נחתכים וצלעותיהם יוצרות בדיוק 6 נקודות חיתוך.

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור
  מקורות:
  • האולימפיאדה לצעירים, תשפ"א, שלב א, כיתות ז-ח שאלה 4

• שאלה

  על דף לבן ציירו משושה קמור ומחומש קמור. מהו המספר הגדול ביותר של חלקים שאליהם הקווים
  בציור יכולים לחלק את הדף?

  נושאים:

  קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשפ"ה, שלב ב שאלה 1

• עבודת טלאים ממשי

  חברות המשפחה ממשפחת וילקינסון הכינו שמיכת טלאים פשוטה, כמתנה קטנה לחג המולד, המורכבת כולה מחתיכות מרובעות באותו גודל, כפי שמוצג באיור. היו חסרות רק ארבע פינות כדי להשלים אותה. מישהו הצביע בפניהן שאם יפרקו את צלב יווני באמצע ואז יחתכו את התפרים לאורך החיבורים הכהים, ארבעת החלקים כולם באותו גודל וצורה יתאימו יחד וייצרו ריבוע. הקורא יודע, מהפתרון באיור `39`, שזה נעשה די בקלות. אבל ג'ורג' וילקינסון הציע להן לפתע את החידה הזו. הוא אמר, "במקום לבחור את הצלב כולו, וליצור את הריבוע מארבעה חלקים שווים, האם תוכלו לחתוך ריבוע שלם וארבעה חלקים שווים שייצרו צלב יווני מושלם?" הפאזל הוא, כמובן, עכשיו די קל.
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 142

• חידת חיתוך קלה

   

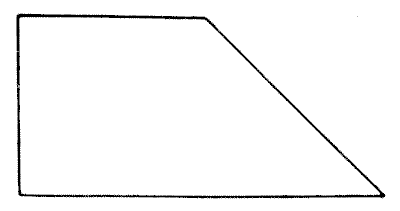
  ראשית, גזרו פיסת נייר או קרטון בצורה המוצגת באיור. ניתן לראות מיד שהפרופורציות הן פשוט אלו של ריבוע המחובר למחצית ריבוע דומה אחר, המחולק באלכסון. החידה היא לחתוך אותו לארבעה חלקים, כולם באותו גודל וצורה בדיוק.

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 146

• חיתוך זוית

   

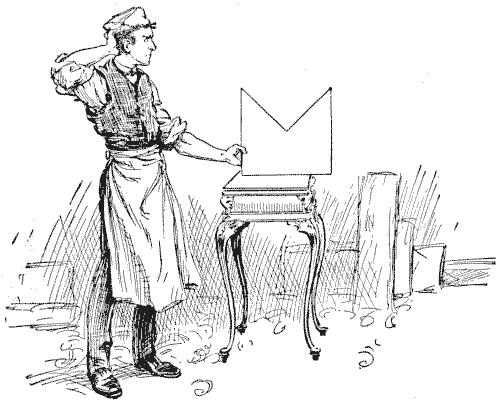
  הצורה שמבלבלת את הנגר באיור מייצגת זווית. ניתן לראות שהמידות שלה הן של ריבוע שהוסר ממנו רבע. החידה היא לחתוך אותה לחמישה חלקים שיתאימו זה לזה וייצרו ריבוע מושלם. אני מציג ניסיון, שפורסם באמריקה, לבצע את המשימה בארבעה חלקים, המבוסס על מה שידוע כ"עיקרון הצעד", אבל זו טעות.  

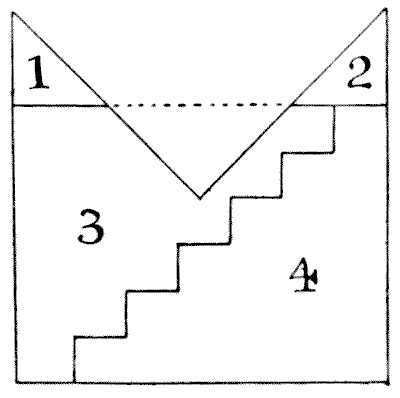
  נאמר לנו תחילה לחתוך את החלקים `1` ו-`2` ולארוז אותם בחלל המשולש המסומן על ידי הקו המקווקו, וכך ליצור מלבן.

  עד כאן טוב ויפה. עכשיו, אנו מונחים ליישם את עקרון הצעד הישן, כפי שמוצג, ועל ידי הזזת החלק `4` צעד אחד למטה, ליצור את הריבוע הנדרש. אבל, לצערי, זה לא מייצר ריבוע: רק מלבן. נקרא לשלושת הצדדים הארוכים של הזווית `84` אינץ' כל אחד. אז, לפני חיתוך הצעדים, המלבן שלנו בשלושה חלקים יהיה `84`×`63`. הצעדים צריכים להיות `10`½ אינץ' בגובה ו-`12` אינץ' ברוחב. לכן, על ידי הזזת צעד אחד למטה אנו מקטינים ב-`12` אינץ' את הצד `84` אינץ' ומגדילים ב-`10`½ אינץ' את הצד `63` אינץ'. לכן המלבן הסופי שלנו חייב להיות `72` אינץ' × `73`½ אינץ', מה שבהחלט אינו ריבוע! העובדה היא שניתן ליישם את עקרון הצעד רק על מלבנים עם צלעות באורכים יחסיים מסוימים. לדוגמה, אם הצד הקצר יותר במקרה זה היה `61` `5/7` (במקום `63`), אז שיטת הצעד תתאים. כי אז הצעדים יהיו `10` `2/7` אינץ' בגובה ו-`12` אינץ' ברוחב. שימו לב ש-`61` `5/7` × `84`= הריבוע של `72`. נכון לעכשיו לא נמצא פתרון בארבעה חלקים, ואני לא מאמין שאפשר למצוא כזה.

  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 150

• הבעיה של הנגר

  לעיתים קרובות הזדמן לי להעיר על התועלת המעשית של חידות, הנובעות מיישום לענייני היומיום של הטריקים הקטנים וה-"קמטים" שאנו לומדים תוך כדי פתרון בעיות שעשוע.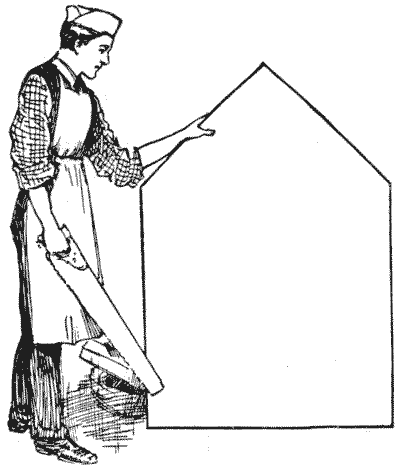 הנגר, באיור, רוצה לחתוך את חתיכת העץ למספר החלקים המינימלי האפשרי כדי ליצור משטח שולחן מרובע, מבלי לבזבז חומר. איך עליו לגשת לעבודה? כמה חלקים תצטרכו?
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 151

• המחומש והריבוע

  מעניין אותי כמה מקוראיי, מבין אלה שלא הקדישו תשומת לב רבה ליסודות הגיאומטריה, יוכלו לצייר מחומש משוכלל, או צורה בעלת חמש צלעות, אם יידרשו לעשות זאת באופן פתאומי. משושה משוכלל, או צורה בעלת שש צלעות, הוא די קל, כי כולם יודעים שכל מה שצריך לעשות הוא לתאר מעגל ואז, לקחת את הרדיוס כאורך אחת הצלעות, ולסמן את שש הנקודות סביב ההיקף. אבל מחומש הוא עניין אחר לגמרי. אז, מכיוון שהחידה שלי קשורה לחיתוך של מחומש משוכלל, אולי כדאי שאקודם כל אראה לקוראים הפחות מנוסים שלי איך יש לצייר צורה זו בצורה נכונה. תארו מעגל וציירו את שני הקווים H B ו-D G, בתרשים, דרך המרכז בזוויות ישרות. כעת מצאו את הנקודה A, באמצע בין C ו-B. לאחר מכן הניחו את חוד המצפן שלכם ב-A ועם המרחק A D תארו את הקשת החותכת את H B ב-E. לאחר מכן הניחו את חוד המצפן שלכם ב-D ועם המרחק D E תארו את הקשת החותכת את ההיקף ב-F. כעת, D F היא אחת הצלעות של המחומש שלכם, ועליכם פשוט לסמן את הצלעות האחרות סביב המעגל. די פשוט כשאתם יודעים איך, אבל אחרת קצת קשה.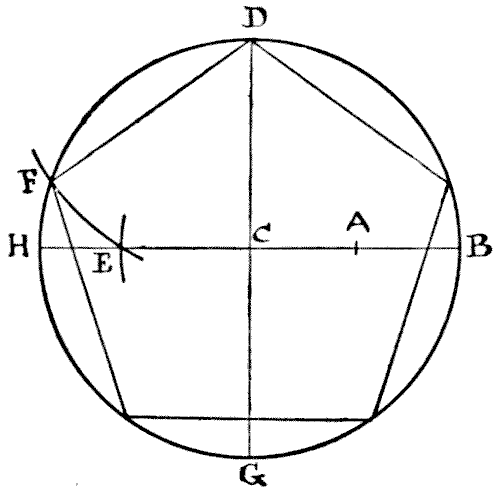 לאחר שיצרתם את המחומש שלכם, החידה היא לחתוך אותו למספר המועט ביותר של חלקים שיתאימו זה לזה וייצרו ריבוע מושלם.
  נושאים:

  גאומטריה -> גאומטריה במישור גאומטריה -> חשבון שטחים קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה גאומטריה -> גאומטריה במרחב -> פאונים -> פאונים משוכללים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 155