לוגיקה

לוגיקה היא חקר ההיגיון והסקת מסקנות תקפה. היא כוללת ניתוח טענות, טיעונים ותהליכים דדוקטיביים. שאלות עשויות לכלול פתרון חידות היגיון, הערכת אמיתותן של טענות מורכבות, שימוש בטבלאות אמת וזיהוי כשלים לוגיים.

הגיון דוברי אמת ושקרנים

  • שיווק של שבת

    הנה מקרה משעשע קטן של שיווק, שלמרות שהוא עוסק במספר רב של פריטי כסף, מוביל לשאלה בעלת אופי שונה לחלוטין. ארבעה זוגות נשואים נסעו לכפר שלהם בשבת בערב האחרון כדי לעשות קניות קטנות. הם היו צריכים להיות מאוד חסכוניים, כי ביחד היו להם רק ארבעים מטבעות שילינג. העניין הוא, אן הוציאה `1`s., מרי הוציאה `2`s., ג'יין הוציאה `3`s., וקייט הוציאה `4`s. הגברים היו קצת יותר פזרניים מנשותיהם, כי נד סמית' הוציא כמו אשתו, טום בראון הוציא פי שניים מאשתו, ביל ג'ונס הוציא פי שלושה מאשתו, וג'ק רובינסון הוציא פי ארבעה מאשתו. בדרך הביתה מישהו הציע שהם יחלקו את מה שנשאר להם באופן שווה ביניהם. זה נעשה, והשאלה המטרידה היא פשוט זו: מה היה שם המשפחה של כל אישה? האם אתה יכול להתאים את ארבעת הזוגות?

    מקורות:

  • מִכְלָא הַצֹּאן

    זהו עובדה מוזרה שהתשובות שניתנות תמיד לכמה מהחידות הידועות ביותר המופיעות בכל ספר קטן של שעשועי בית שפורסם בחמישים או מאה השנים האחרונות הן או בלתי מספקות לחלוטין או שגויות בבירור. עם זאת, נראה שאף אחד לא מבחין בפגמים שלהן. הנה דוגמה: - לחקלאי היה מכלאה העשויה מחמישים גדרות, המסוגלת להכיל רק מאה כבשים. נניח שהוא רצה להגדיל אותו מספיק כדי להכיל כפול ממספר זה, כמה גדרות נוספות הוא צריך? מקורות:

  • חידת החגב

    הועלתה סברה שהחידה הזו הייתה חביבה מאוד על החניכים הצעירים של הסיטי של לונדון במאות השש-עשרה והשבע-עשרה. הקוראים בוודאי הבחינו בחגב הפליז המוזר בבורסה המלכותית. יצור ארוך שנים זה ניצל משריפות `1666` ו-`1838`. החגב, כדרכו, היה סמל של סר תומס גרשם, סוחר מכולת, שמת בשנת `1579`, ומסיבה זו הוא שימש כסמל על ידי מכולת באופן כללי. למרבה הצער עבור האגדה לגבי מקורה, החידה הופקה על ידי עצמי רק בשנת `1900`. על שנים עשר מתוך שלושה עשר הדיסקים השחורים מונחים אסימונים ממוספרים או חגבים. החידה היא להפוך את סדרם, כך שיקראו, `1, 2, 3, 4` וכו', בכיוון ההפוך, כאשר הדיסק הריק נשאר באותו מיקום כמו עכשיו. הזיזו אחד בכל פעם בכל סדר, או לדיסק הריק הסמוך או על ידי קפיצה מעל חגב אחד, כמו המהלכים בדמקה. ניתן לבצע את המהלכים או הקפיצות בכל כיוון שאפשרי בכל עת. מהם מספר המהלכים המועט ביותר שבו ניתן לעשות זאת?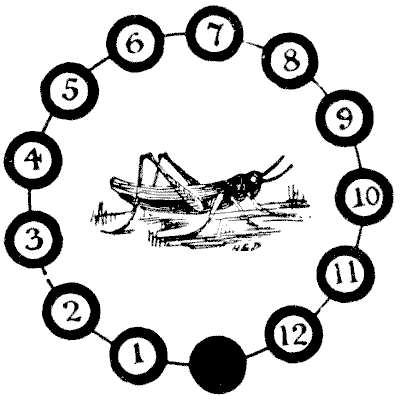 מקורות:

  • קושי בבית דירות

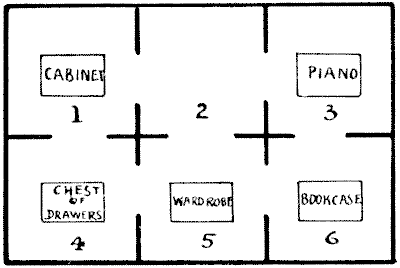    משפחת דובסון שכרה דירות בסלוקום-און-סי. היו שישה חדרים באותה קומה, כולם מחוברים, כפי שמוצג בתרשים. החדרים שהם לקחו היו מספרים `4, 5`, ו-`6`, כולם פונים לים. אבל התעוררה בעיה קטנה. מר דובסון התעקש שהפסנתר וארון הספרים יחליפו חדרים. זה היה ערמומי, כי משפחת דובסון לא הייתה מוזיקלית, אבל הם רצו למנוע מכל אחד אחר לנגן בכלי הנגינה. עכשיו, החדרים היו קטנים מאוד ופריטי הריהוט שצוינו היו גדולים מאוד, כך שלא ניתן היה להכניס שניים מהפריטים הללו לאף חדר באותו זמן. איך ניתן לבצע את ההחלפה עם מינימום עבודה? נניח, לדוגמה, שאתה מעביר תחילה את הארון לבגדים למספר `2`; אז אתה יכול להעביר את ארון הספרים למספר `5` ואת הפסנתר למספר `6`, וכן הלאה. זו חידה מרתקת, אבל לבעלת הבית היו סיבות לא להעריך אותה. נסה לפתור את הקושי שלה במספר המינימלי האפשרי של העברות עם אסימונים על דף נייר. מקורות:

  • חידת מוסך המכוניות

     

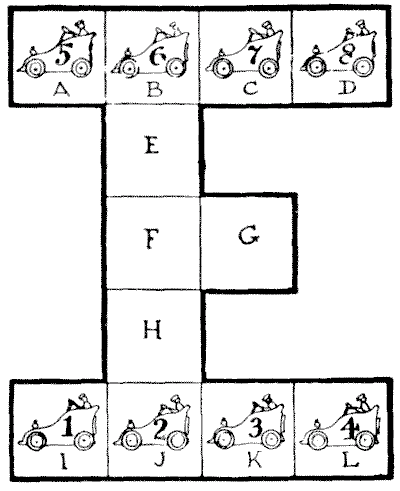
    הקשיים של בעל מוסך מוסבים למעין בילוי שיש בו קסם מיוחד. כל מה שצריך זה להכין תוכנית או דיאגרמה פשוטה על דף נייר או קרטון ולמספר שמונה אסימונים, מ-`1` עד `8`. אז משפחה שלמה יכולה להיכנס לתחרות משעשעת כדי למצוא את הפתרון הטוב ביותר לקושי.

    האיור מייצג את תוכנית מוסך המכוניות, עם מקום לשתים עשרה מכוניות. אבל השטח מצומצם בצורה לא נוחה, ולכן הבעלים נתקל לעתים קרובות במבוכה רבה. נניח, למשל, ששמונה המכוניות הממוספרות מ-`1` עד `8` נמצאות במקומות המוצגים, איך ניתן להזיז אותן בצורה המהירה ביותר כך ש-`1, 2, 3` ו-`4` יחליפו מקומות עם `5, 6, 7` ו-`8` — כלומר, כשהמספרים עדיין רצים משמאל לימין, כפי שהם כרגע, אבל השורה העליונה הוחלפה בשורה התחתונה? מהו המספר הקטן ביותר של מהלכים אפשריים?

    מכונית אחת זזה בכל פעם, וכל מרחק נחשב למהלך אחד. כדי למנוע אי הבנות, מקומות העצירה מסומנים בריבועים, ויכולה להיות רק מכונית אחת בריבוע בכל פעם.

    מקורות:

  • סובב את החוף

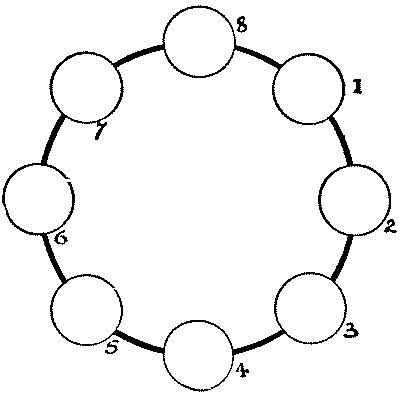    הנה חידה שלדעתי תהיה משעשעת כמו שהיא מלמדת. נתון לנו מעגל של שמונה עיגולים. כאשר עיגול `8` ריק, עלינו לכתוב את שמה של עיר נמל בת שבע אותיות בממלכה המאוחדת באופן הזה. געו בעיגול ריק עם העיפרון שלכם, ואז קפצו מעל שני עיגולים בכל כיוון מסביב למעגל, וכתבו את האות הראשונה. לאחר מכן געו בעיגול ריק אחר, קפצו מעל שני עיגולים, וכתבו את האות השנייה. המשיכו באופן דומה עם שאר האותיות בסדר הנכון שלהן עד שתשלימו את המילה. לדוגמה, נניח שנבחר ב-"Glasgow," ונמשיך כדלקמן: `6`—`1, 7`—`2, 8`—`3, 7`—`4, 8`—`5`, מה שאומר שאנחנו נוגעים ב-`6`, קופצים מעל `7`, וכותבים "G" על `1`; לאחר מכן נוגעים ב-`7`, קופצים מעל `8` ו-`1`, וכותבים "l" על `2`; וכן הלאה. יתברר שאחרי שכתבנו את חמש האותיות הראשונות - "Glasg" - כמו לעיל, אנחנו לא יכולים להמשיך הלאה. או שיש משהו לא בסדר עם "Glasgow," או שלא הצלחנו לבצע את הקפיצות שלנו כראוי. האם תוכלו לרדת לשורש התעלומה? מקורות:

  • חידת ההחלפה

    הנה חידה קטנה ומשעשעת עם העברת חיילים. אתה צריך רק שנים עשר חיילים—שישה מצבע אחד, המסומנים A, C, E, G, I ו-K, והשישה האחרים מסומנים B, D, F, H, J ו-L. אתה מניח אותם תחילה על הדיאגרמה, כפי שמוצג באיור, והחידה היא להביא אותם לסדר אלפביתי רגיל, כדלקמן:—

    A B C D
    E F G H
    I J K L

    המהלכים מתבצעים על ידי החלפות של צבעים מנוגדים העומדים על אותו קו. כך, G ו-J יכולים להחליף מקומות, או F ו-A, אבל אינך יכול להחליף את G ו-C, או F ו-D, מכיוון שבמקרה אחד שניהם לבנים ובמקרה השני שניהם שחורים. האם אתה יכול להביא את הסידור הנדרש בשבע עשרה החלפות?

     

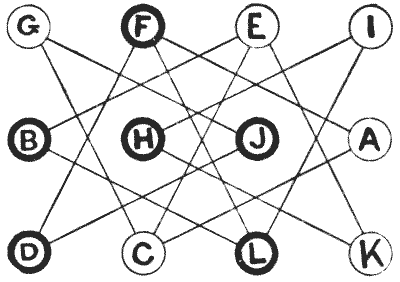
    אי אפשר לעשות זאת בפחות מהלכים. החידה באמת הרבה יותר קלה ממה שהיא נראית, אם תוקפים אותה כראוי.

    מקורות:

  • בנים ובנות

    אם תסמנו עשרה חלוקות על דף נייר כדי לייצג את הכיסאות, ותשתמשו בשמונה אסימונים ממוספרים עבור הילדים, יהיה לכם בילוי מרתק. תנו למספרים האי-זוגיים לייצג בנים ולמספרים הזוגיים בנות, או שתוכלו להשתמש באסימונים משני צבעים, או במטבעות.

    החידה היא להסיר שני ילדים היושבים בכיסאות סמוכים ולהניח אותם בשני כיסאות ריקים, כאשר הם מחליפים צדדים תחילה; לאחר מכן הסירו זוג ילדים שני מכיסאות סמוכים והניחו אותם בשני הכיסאות הפנויים כעת, כשהם מחליפים צדדים; וכן הלאה, עד שכל הבנים יהיו ביחד וכל הבנות ביחד, כאשר שני הכיסאות הריקים בקצה אחד כמו עכשיו. כדי לפתור את החידה, עליכם לעשות זאת בחמישה מהלכים. שני הילדים חייבים תמיד להילקח מכיסאות הצמודים זה לזה; וזכרו את הנקודה החשובה של החלפת הצדדים בין שני הילדים, שכן זהו המאפיין הייחודי של החידה. על ידי "החלפת צדדים" אני פשוט מתכוון שאם, לדוגמה, תזיזו תחילה את `1` ו-`2` לכיסאות הריקים, אז הכיסא הראשון (החיצוני) יאוכלס על ידי `2` והשני על ידי `1`. 

    מקורות:

  • סידור קופסאות הריבה

    קרה שראיתי ילדה קטנה ממיינת ריבות בארון עבור אמה. היא הניחה כל סוג ריבה בנפרד על המדפים. שמתי לב שהיא לקחה צנצנת שזיפים ביד אחת וצנצנת דומדמניות ביד השנייה והחליפה ביניהן; אחר כך היא החליפה תות שדה עם פטל, וכן הלאה. היה מעניין לראות כמה טרחה מיותרת היא נתנה לעצמה על ידי ביצוע יותר החלפות ממה שהיה צורך, וחשבתי שזה יכול להפוך לחידה טובה.

     

    כפי שניתן לראות באיור, דורותי הקטנה צריכה לתפעל עשרים וארבע קופסאות ריבה גדולות במספר תאים תואם. היא רוצה לסדר אותן בסדר מספרי נכון—כלומר, `1, 2, 3, 4, 5, 6` על המדף העליון, `7, 8, 9, 10, 11, 12` על המדף הבא, וכן הלאה. עכשיו, אם היא תמיד לוקחת קופסה אחת ביד ימין ואחת ביד שמאל ומחליפה ביניהן, כמה מההחלפות האלה יהיו נחוצות כדי לסדר את כל קופסאות הריבה בסדר הנכון? באופן טבעי היא תחליף קודם את `1` ואת `3`, אחר כך את `2` ואת `3`, ואז יהיו לה שלוש הקופסאות הראשונות במקומן. איך היית מייעץ לה להמשיך מכאן? הניחו כמה אסימונים ממוספרים על דף נייר המחולק למשבצות עבור התאים, ותגלו שזו חידה משעשעת.

    מקורות:

  • מסע האופניים

    שני רוכבי אופניים התייעצו במפת דרכים לקראת טיול קצר משותף. העיגולים מייצגים ערים, וכל הדרכים הטובות מיוצגות על ידי קווים. הם מתחילים מהעיר עם הכוכב, ועליהם להשלים את הטיול שלהם ב-E. אבל לפני שהם מגיעים לשם הם רוצים לבקר בכל עיר אחרת פעם אחת, ורק פעם אחת. זו הבעיה. מר ספייסר אמר, "אני בטוח שנוכל למצוא דרך לעשות זאת;" אבל מר מגס השיב, "בשום אופן, אני בטוח." עכשיו, מי מהם צדק? קחו את העיפרון שלכם ובדקו אם תוכלו למצוא דרך לעשות זאת. כמובן שעליכם להישאר בדרכים המצוינות.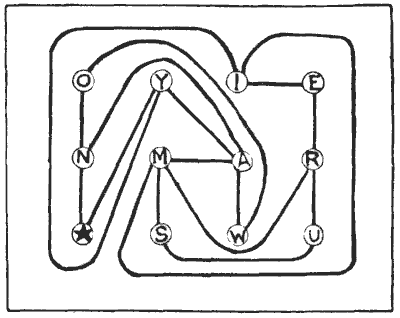 מקורות: