לוגיקה
לוגיקה היא חקר ההיגיון והסקת מסקנות תקפה. היא כוללת ניתוח טענות, טיעונים ותהליכים דדוקטיביים. שאלות עשויות לכלול פתרון חידות היגיון, הערכת אמיתותן של טענות מורכבות, שימוש בטבלאות אמת וזיהוי כשלים לוגיים.
הגיון דוברי אמת ושקרנים-
הטיול הגדול
אחת החידות היומיומיות של החיים היא תכנון מסלולים. אם אתם יוצאים לחופשה על אופניים, או לטיול מוטורי, תמיד עולה השאלה כיצד לנצל את הזמן והמשאבים שלכם בצורה הטובה ביותר. החלטתם להגיע למקום מסוים, לכלול ביקורים בעיר כזו וכזו, לנסות לראות משהו מעניין במיוחד במקום אחר, ואולי לנסות לבקר חבר ותיק בנקודה שלא תוציא אתכם בהרבה מהדרך. אז אתם צריכים לתכנן את המסלול שלכם כדי להימנע מכבישים גרועים, אזורים לא מעניינים, ואם אפשר, מהצורך לחזור באותה דרך שבה נסעתם. עם מפה לפניכם, ניגשים לפתרון החידה המעניינת. אציג לכם שאלה קטנה המבוססת על קווים אלה.
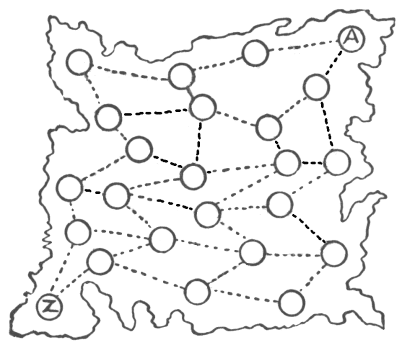
אני מציג מפה גסה של מדינה—אין צורך לומר איזו מדינה—העיגולים מייצגים ערים והקווים המקווקווים את מסילות הברזל המחברות ביניהן. עכשיו, בעיר המסומנת A חי אדם שנולד שם, ובמשך כל חייו מעולם לא עזב את מקום הולדתו. מנעוריו הוא היה חרוץ מאוד, דבק בעקביות במקצועו, ולא היה לו רצון לשוטט בחוץ. עם זאת, בהגיעו לגיל חמישים הוא החליט לראות קצת מהמדינה שלו, ובמיוחד לבקר חבר ותיק מאוד שגר בעיר המסומנת Z. מה שהוא הציע היה כזה: שהוא יתחיל מביתו, ייכנס לכל עיר פעם אחת בלבד, ויסיים את מסעו ב-Z. מכיוון שהוא החליט לבצע את הטיול הגדול הזה ברכבת בלבד, הוא התקשה קצת לתכנן את המסלול שלו, אבל בסופו של דבר הוא הצליח לעשות זאת. איך הוא הצליח? אל תשכחו שצריך לבקר בכל עיר פעם אחת, ולא יותר מפעם אחת.
 מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
מקורות:נושאים:קומבינטוריקה -> גאומטריה קומבינטורית קומבינטוריקה -> תורת הגרפים לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 250
-
מים, גז וחשמל
ישנם כחצי תריסר חידות, עתיקות כימי ההיסטוריה, שצצות ועולות תדיר, וכמעט שאין חודש בשנה שלא מביא עמו פניות בנוגע לפתרונן. מדי פעם אחת מהן, שאדם חשב שהיא הר געש כבוי, מתפרצת בצורה מפתיעה. קיבלתי מספר יוצא דופן של מכתבים בנוגע לחידה העתיקה שכיניתי "מים, גז וחשמל". היא עתיקה בהרבה מתאורת חשמל, או אפילו גז, אבל הלבוש החדש מעדכן אותה. החידה היא להניח מים, גז וחשמל, מ-W, G ו-E, לכל אחד משלושת הבתים, A, B ו-C, מבלי שאף צינור יחצה צינור אחר. קחו את העיפרון וציירו קווים המראים כיצד יש לעשות זאת. עד מהרה תמצאו את עצמכם נתקלים בקשיים.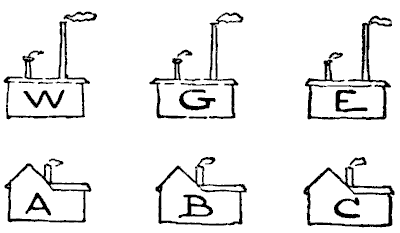 מקורות:
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 251
-
חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים
אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים
החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה?
מקורות:נושאים:אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 262
-
החלון של האב המנזר
לפני שנים רבות, האב המנזר מסנט אדמונדסברי, כתוצאה מ"מסירות חזקה מדי לראשו," חלה ולא היה מסוגל לעזוב את מיטתו. כששכב ער, מטלטל את ראשו באי שקט מצד לצד, הנזירים הקשובים הבחינו שמשהו מטריד את מחשבותיו; אך איש לא העז לשאול מה זה יכול להיות, כי האב המנזר היה בעל אופי קשוח, ומעולם לא סבל סקרנות. לפתע קרא לאב ג'ון, והנזיר המכובד ההוא מיהר למיטתו.
"אב ג'ון," אמר האב המנזר, "האם אתה יודע שנולדתי לעולם הנורא הזה בערב חג המולד?
"הנזיר הנהן בהסכמה.
"והאם לא אמרתי לך לעתים קרובות, שנולדתי בערב חג המולד, שאין לי אהבה לדברים שהם אי-זוגיים? תסתכל שם!"
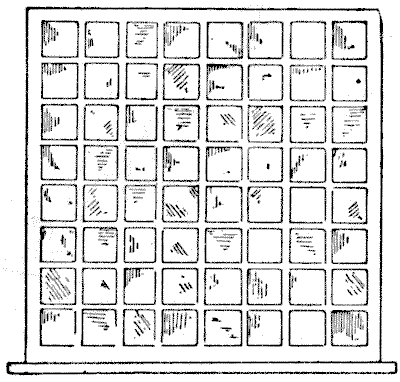
האב המנזר הצביע על חלון המעונות הגדול, שממנו אני נותן סקיצה. הנזיר הביט, והיה נבוך.
"האם אינך רואה ששישים וארבעת האורות מסתכמים למספר זוגי אנכית ואופקית, אך כל הקווים האלכסוניים, למעט ארבעה עשר, הם מספר שהוא אי-זוגי? מדוע זה?"
"אכן, אדוני האב המנזר, זה טבע הדברים, ואי אפשר לשנות זאת."
"לא, אבל זה יש ישתנה. אני מצווה עליך שחלק מהאורות ייחסמו היום, כך שלכל קו יהיה מספר זוגי של אורות. ראה שזה נעשה ללא דיחוי, שמא המרתפים יינעלו לחודש וצרות קשות אחרות יפקדו אותך."
אב ג'ון היה חסר אונים, אך לאחר התייעצות עם מישהו שהיה בקיא בתעלומות מוזרות, נמצאה דרך לספק את גחמתו של האב המנזר. אילו אורות נחסמו, כך שאלה שנותרו הסתכמו למספר זוגי בכל קו אופקית, אנכית ואלכסונית, תוך גרימת ההפרעה המינימלית האפשרית לאור?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 292
-
שמונה מלכות
המלכה היא ללא ספק הכלי החזק ביותר על לוח השחמט. אם תניח אותה על אחד מארבעת הריבועים במרכז הלוח, היא תוקפת לא פחות מעשרים ושבעה ריבועים אחרים; ואם תנסה להחביא אותה בפינה, היא עדיין תתקוף עשרים ואחד ריבועים. ניתן להניח שמונה מלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וזוהי חידה ותיקה (שהועלתה לראשונה על ידי נאוק ב-`1850`, ויש לה ספרות משלה) לגלות בכמה דרכים שונות ניתן לעשות זאת. אני מראה דרך אחת בתרשים, ויש בסך הכל שתים עשרה דרכים שונות במהותן. שנים עשר אלה מניבים תשעים ושתיים דרכים אם אנו רואים היפוכים ושיקופים כשונים. התרשים הוא במידה מסוימת סידור סימטרי. אם תהפוך את הדף, הוא ישחזר את עצמו בדיוק; אבל אם תסתכל עליו כשאחד הצדדים האחרים בתחתית, תקבל דרך אחרת שאינה זהה. ואז אם תשקף את שתי הדרכים האלה במראה, תקבל עוד שתי דרכים. כעת, כל אחד-עשר הפתרונות האחרים אינם סימטריים, ולכן ניתן להציג כל אחד מהם בשמונה דרכים על ידי היפוכים ושיקופים אלה. כך יובן מדוע שנים עשר הפתרונות השונים במהותם מניבים רק תשעים ושניים סידורים, כפי שאמרתי, ולא תשעים וששה, כפי שהיה קורה אילו כל שנים עשר לא היו סימטריים. כדאי שתהיה הבנה ברורה בעניין ההיפוכים והשיקופים כאשר עוסקים בחידות על לוח השחמט. האם הקורא יכול להניח את שמונה המלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וכך שאף שלוש מלכות לא יהיו בקו ישר בכל כיוון אלכסוני? מבט נוסף בתרשים יראה שהסידור הזה לא יענה על התנאים, כי בשני הכיוונים המצוינים בקווים המקווקווים יש שלוש מלכות בקו ישר. יש רק דרך אחת מתוך שתים עשרה הדרכים הבסיסיות שתפתור את החידה. האם אתה יכול למצוא את זה?
מקורות:
האם הקורא יכול להניח את שמונה המלכות על הלוח כך שאף מלכה לא תתקוף מלכה אחרת, וכך שאף שלוש מלכות לא יהיו בקו ישר בכל כיוון אלכסוני? מבט נוסף בתרשים יראה שהסידור הזה לא יענה על התנאים, כי בשני הכיוונים המצוינים בקווים המקווקווים יש שלוש מלכות בקו ישר. יש רק דרך אחת מתוך שתים עשרה הדרכים הבסיסיות שתפתור את החידה. האם אתה יכול למצוא את זה?
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 300
-
קוביות האותיות - שלושים ושש
 האיור מייצג קופסה המכילה שלושים ושש קוביות אותיות. החידה היא לסדר מחדש את הקוביות כך שאף A לא יהיה בקו אנכי, אופקי או אלכסוני עם A אחר, אף B עם B אחר, אף C עם C אחר, וכן הלאה. תגלו שאי אפשר להכניס את כל האותיות לקופסה בתנאים אלה, אך העניין הוא למקם כמה שיותר. כמובן שאסור להשתמש באותיות אחרות מלבד אלה המוצגות.
מקורות:
האיור מייצג קופסה המכילה שלושים ושש קוביות אותיות. החידה היא לסדר מחדש את הקוביות כך שאף A לא יהיה בקו אנכי, אופקי או אלכסוני עם A אחר, אף B עם B אחר, אף C עם C אחר, וכן הלאה. תגלו שאי אפשר להכניס את כל האותיות לקופסה בתנאים אלה, אך העניין הוא למקם כמה שיותר. כמובן שאסור להשתמש באותיות אחרות מלבד אלה המוצגות.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 305
-
חידת מלכות ורץ
יובחן שכל משבצת בלוח היא תפוסה או מותקפת. החידה היא להחליף רץ בצריח באותה המשבצת, ואז להניח את ארבע המלכות על משבצות אחרות כך שכל משבצת שוב תהיה תפוסה או מותקפת.
מקורות:
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 313
-
הצלב הדרומי

באיור לעיל יש לנו חמישה כוכבי לכת ושמונים ואחד כוכבים קבועים, כאשר חמישה מהאחרונים מוסתרים על ידי כוכבי הלכת. ניתן לראות שכל כוכב, למעט עשרת הכוכבים שיש להם נקודה שחורה במרכזם, נמצא בקו ישר, אנכית, אופקית או באלכסון, עם לפחות אחד מכוכבי הלכת. החידה היא לסדר מחדש את כוכבי הלכת כך שכל הכוכבים יהיו בקו אחד עם אחד או יותר מהם.
בסידור מחדש של כוכבי הלכת, כל אחד מחמשתם עשוי לנוע פעם אחת בקו ישר, בכל אחד משלושת הכיוונים שהוזכרו. הם, כמובן, יסתירו חמישה כוכבים אחרים במקום אלה המכוסים כעת.
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 314
-
שומרי האבירים
האביר הוא הקומיקאי הנמוך חסר האחריות של לוח השחמט. "הוא נוכל מאוד לא בטוח, מתגנב ומדכא," אומר סופר אמריקאי. "הוא יכול לזוז רק שני ריבועים, אך מפצה על כמות התנועה שלו באיכותה, שכן הוא יכול לקפוץ ריבוע אחד הצידה ואחד קדימה בו זמנית, כמו חתול; יכול לעמוד על רגל אחת באמצע הלוח ולקפוץ לכל אחד משמונת הריבועים שהוא בוחר; יכול לעלות על צד אחד של גדר ולהשמיץ שלושה או ארבעה אנשים בצד השני; יש לו דרך מעוררת התנגדות להכניס את עצמו למקומות בטוחים שבהם הוא יכול להפחיד את המלך ולאלץ אותו לזוז, ואז לטרוף מלכה. לרוע טהור אין לאביר שווה, וכאשר אתה רודף אחריו מחור אחד הוא קופץ לאחר." נעשו ניסיונות שוב ושוב להשיג הגדרה קצרה, פשוטה ומדויקת של תנועת האביר—ללא הצלחה. זה באמת מורכב מלהזיז ריבוע אחד כמו צריח, ואז ריבוע אחר כמו רץ—שני הפעולות נעשות בקפיצה אחת, כך שלא משנה אם הריבוע הראשון שעוברים עליו תפוס על ידי כלי אחר או לא. זו, למעשה, התנועה הקופצת היחידה בשחמט. אבל קשה ככל שיהיה להגדיר, ילד יכול ללמוד את זה על ידי הסתכלות תוך מספר דקות.
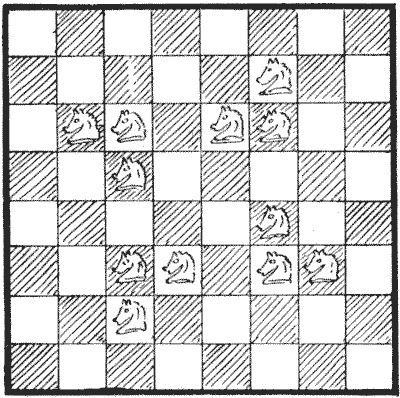
הראיתי בתרשים כיצד ניתן להציב שנים עשר אבירים (המספר הקטן ביותר האפשרי שיבצע את המשימה) על לוח השחמט כך שכל ריבוע יהיה או תפוס או מותקף על ידי אביר. בחן כל ריבוע בתורו, ותגלו שזה כך. כעת, החידה במקרה זה היא לגלות מהו המספר הקטן ביותר האפשרי של אבירים הנדרש כדי שכל ריבוע יהיה או תפוס או מותקף, וכל אביר מוגן על ידי אביר אחר. ואיך הייתם מסדרים אותם? יתברר שמתוך שנים עשר המוצגים בתרשים רק ארבעה מוגנים כך על ידי היותם במרחק מהלך של אביר מאביר אחר.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 319
-
מסע הצריח
אני קורא לחידה הזו "מסע הצריח", מכיוון שהמילה "tour" (הנגזרת מגלגל של חרט) מרמזת שאנו חוזרים לנקודה ממנה יצאנו, ואנו לא עושים זאת במקרה הזה. לא נהיה מרוצים מסיור חג מודרך אישית שהסתיים בכך שהשאיר אותנו, למשל, באמצע הסהרה. הצריח כאן עושה עשרים ואחד מהלכים, שבמהלכם הוא מבקר בכל משבצת בלוח פעם אחת בלבד, ועוצר במשבצת המסומנת `10` בסוף המהלך העשירי שלו, ומסתיים במשבצת המסומנת `21`. שני מהלכים רצופים אינם יכולים להתבצע באותו כיוון - כלומר, עליך לבצע פנייה לאחר כל מהלך.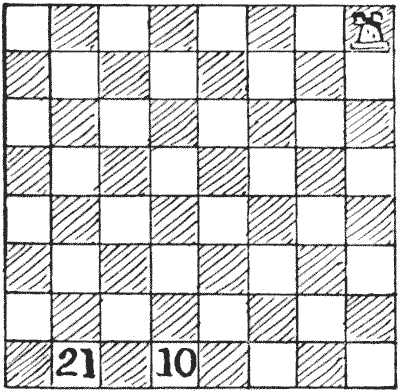 מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים
מקורות:נושאים:לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות חידות ורבוסים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 321