אריתמטיקה

אריתמטיקה היא ענף יסודי במתמטיקה העוסק במספרים ובפעולות הבסיסיות: חיבור, חיסור, כפל וחילוק. שאלות כוללות ביצוע פעולות אלו, הבנת תכונות מספרים (כמו שלמים, שברים, עשרוניים) ופתרון בעיות מילוליות קשורות.

שברים אחוזים חילוק עם שארית

  • לתפוס את הגנב

    "ובכן, שוטר," אמר סנגור הנאשם בחקירה נגדית, "אתה אומר שהאסיר היה בדיוק עשרים ושבעה צעדים לפניך כשאתה התחלת לרוץ אחריו?"

    "כן, אדוני."

    "ואתה נשבע שהוא עושה שמונה צעדים לחמישה שלך?"

    "זה נכון."

    "אם כך אני שואל אותך, שוטר, כאדם אינטליגנטי, להסביר איך בכלל תפסת אותו, אם זה המקרה?"

    "ובכן, אתה מבין, יש לי פסיעה ארוכה יותר. למעשה, שניים מהצעדים שלי שווים באורכם לחמישה של האסיר. אם תחשב את זה, תגלה שמספר הצעדים שהייתי צריך יביא אותי בדיוק למקום שבו תפסתי אותו."

    כאן ביקש חבר המושבעים הראשי כמה דקות כדי לחשב את מספר הצעדים שהשוטר היה צריך לעשות. האם גם אתם יכולים לומר כמה צעדים השוטר היה צריך כדי לתפוס את הגנב?

    מקורות:

  • הבחירות במאדלטאון

    בבחירות הפרלמנטריות האחרונות במאדלטאון נספרו `5,473` קולות. הליברל נבחר ברוב של `18` על פני השמרן, ברוב של `146` על פני העצמאי וברוב של `575` על פני הסוציאליסט. האם תוכל לתת כלל פשוט לחישוב מספר הקולות שנספרו עבור כל מועמד? מקורות:

  • החידה של האב המנזר

    חידונאי האנגלי הראשון ששמו הגיע אלינו היה איש יורקשייר — לא אחר מאשר אלקווין, אב המנזר מקנטרברי (A.D. `735-804`). הנה חידה קטנה מכתביו, שלפחות מעניינת בשל עתיקותה. "אם `100` בושלים של תירס חולקו בין `100` אנשים באופן שכל גבר קיבל שלושה בושלים, כל אישה שניים, וכל ילד חצי בושל, כמה גברים, נשים וילדים היו שם?"

    כעת, ישנן שש תשובות נכונות שונות, אם נחריג מקרה שבו לא יהיו נשים. אבל נניח שהיו פי חמישה נשים מגברים, אז מה הפתרון הנכון?

    מקורות:

  • טעות של מדפיס

    במאמר מסוים, מדפיס היה צריך לסדר את הספרות `5^4xx2^3`, אשר כמובן, משמעותו שהחזקה הרביעית של `5` (`625`) צריכה להיות מוכפלת בחזקה השלישית של `2` (`8`), שהמכפלה שלהם היא `5,000`. אבל הוא הדפיס את `5^4xx2^3` כ- `5\ 4\ 2\ 3`, וזה לא נכון. האם תוכלו למקם ארבע ספרות באופן המוצג, כך שזה יהיה נכון באותה מידה אם המדפיס יסדר אותן כראוי או יעשה את אותה טעות?

    מקורות:

  • הקפת הריבועים

     

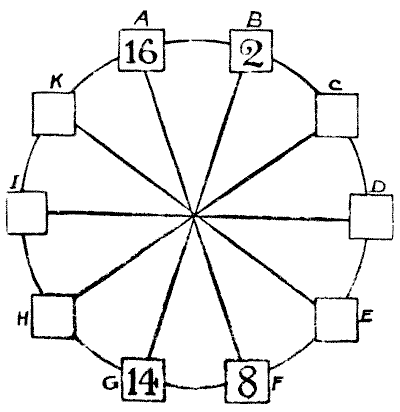
    החידה היא להציב מספר שונה בכל אחד מעשרת הריבועים כך שסכום ריבועי כל שני מספרים סמוכים יהיה שווה לסכום ריבועי שני המספרים הנמצאים בדיוק מולם במעגל. ארבעת המספרים המוצבים כדוגמאות חייבים להישאר במקומם. ריבוע של `16` הוא `256`, וריבוע של `2` הוא `4`. חברו אותם יחד, והתוצאה היא `260`. כמו כן—ריבוע של `14` הוא `196`, וריבוע של `8` הוא `64`. גם אלה יחד יוצרים `260`. עכשיו, באותו אופן בדיוק, B ו-C צריכים להיות שווים ל-G ו-H (הסכום לא בהכרח יהיה `260`), A ו-K ל-F ו-E, H ו-I ל-C ו-D, וכן הלאה, עם כל שני ריבועים סמוכים במעגל.

    כל שעליכם לעשות הוא למלא את ששת המספרים הנותרים. שברים אינם מותרים, ואני אראה שאף מספר לא צריך להכיל יותר משתי ספרות.

    מקורות:

  • כפל פשוט

    אם נמספר שישה כרטיסים `1, 2, 4, 5, 7`, ו-`8`, ונניח אותם על השולחן בסדר הזה:—

    `1\ \ \ 4\ \ \ 2\ \ \ 8\ \ \ 5\ \ \ 7`

    אנו יכולים להדגים שכדי להכפיל ב-`3` כל מה שצריך זה להעביר את ה-`1` לקצה השני של השורה, וזהו. התשובה היא `428571`. האם תוכלו למצוא מספר שכאשר מכפילים אותו ב-`3` ומחלקים ב-`2`, התשובה תהיה זהה כאילו הסרנו את הכרטיס הראשון (שבמקרה הזה צריך להיות `3`) מתחילת השורה לסופה?

    מקורות:

  • חילוק פשוט

    לפעמים שאלה פשוטה מאוד באריתמטיקה אלמנטרית תגרום למבוכה רבה. לדוגמה, אני רוצה לחלק את ארבעת המספרים, `701, 1,059, 1,417`, ו-`2,312`, במספר הגדול ביותר האפשרי שישאיר את אותה שארית בכל מקרה. איך אני אמור להתחיל לעבוד? כמובן, על ידי מערכת ניסויים מייגעת אפשר עם הזמן לגלות את התשובה, אבל יש שיטה די פשוטה לעשות זאת אם רק תוכל למצוא אותה. מקורות:

  • הקמצן הספרדי

    בעיירה קטנה בקסטיליה החדשה חי פעם קמצן ידוע בשם דון מנואל רודריגז. אהבתו לכסף הושוותה רק לתשוקה עזה לבעיות אריתמטיות. חידות אלה עסקו בדרך כלל באופן כזה או אחר באוצרותיו שנצברו, והוצעו על ידו אך ורק כדי שיוכל ליהנות מלפתור אותן בעצמו. למרבה הצער, רק מעטות מהן שרדו, וכאשר טיילתי בספרד, ואספתי חומר לעבודה מוצעת על "הבצל הספרדי כגורם לשקיעה לאומית", גיליתי רק מעטות מאוד. אחת מהן עוסקת בשלוש הקופסאות המופיעות בפורטרט האותנטי המצורף. כל קופסה הכילה מספר שונה של דובלוני זהב. ההפרש בין מספר הדובלונים בקופסה העליונה למספר בקופסה האמצעית היה זהה להפרש בין המספר בקופסה האמצעית למספר בקופסה התחתונה. ואם תכולתן של שתיים כלשהן מהקופסאות היו מאוחדות, הן היו יוצרות מספר ריבועי. מהו המספר הקטן ביותר של דובלונים שיכול היה להיות באחת מהקופסאות? מקורות:

  • חמשת השודדים

    חמשת השודדים הספרדים, אלפונסו, בניטו, קרלוס, דייגו ואסטבן, ספרו את שללם לאחר פשיטה, כאשר התגלה שהם שדדו יחד בדיוק `200` דובלונים. אחד מהחבורה ציין שאם לאלפונסו יהיה פי שנים עשר, לבניטו פי שלושה, לקרלוס אותו סכום, לדייגו חצי מהסכום ולאסטבן שליש מהסכום, עדיין יהיו להם יחד בדיוק `200` דובלונים. כמה דובלונים היו לכל אחד?

    ישנן תשובות נכונות רבות באותה מידה לשאלה זו. הנה אחת מהן:

    A 6 × 12 = 72
    B 12 × 3 = 36
    C 17 × 1 = 17
    D 120 × ½ = 60
    E 45 × 1/3 = 15
      200       200

    החידה היא לגלות בדיוק כמה תשובות שונות יש, בהנחה שלכל אחד היה משהו ושאסור שיהיה כסף חלקי — רק דובלונים בכל מקרה.

    בעיה זו, שניסוחה שונה במקצת, הוצגה על ידי טרטליה (נפטר ב-`1559`), והוא החמיא לעצמו שהוא מצא פתרון אחד; אבל מתמטיקאי צרפתי ידוע (M.A. Labosne), בעבודה מהעת האחרונה, אומר שקוראיו יופתעו כאשר הוא מבטיח להם שיש `6,639` תשובות נכונות שונות לשאלה. האם זה כך? כמה תשובות יש?

    מקורות:

  • הבעיה של סתת האבנים

    לסתת אבנים היה פעם מספר גדול של קוביות אבן בחצר שלו, כולן באותו גודל בדיוק. היו לו כמה הרגלים קטנים דמיוניים מאוד, ואחד הרעיונות המוזרים שלו היה לשמור את הבלוקים האלה מוערמים בערימות מעוקבות, כך שאין שתי ערימות שמכילות את אותו מספר בלוקים. הוא גילה בעצמו (עובדה שידועה היטב למתמטיקאים) שאם הוא היה לוקח את כל הבלוקים הכלולים במספר כלשהו של ערימות בסדר רגיל, החל מהקוביה הבודדת, הוא תמיד יכול היה לסדר אותם על הקרקע כדי ליצור ריבוע מושלם. זה יהיה ברור לקורא, מכיוון שבלוק אחד הוא ריבוע, `1+8 = 9` הוא ריבוע, `1+8+27=36` הוא ריבוע, `1+8+27+64=100` הוא ריבוע, וכן הלאה. למעשה, סכום כל מספר של קוביות עוקבות, החל תמיד מ-`1`, הוא בכל מקרה מספר ריבועי.

    יום אחד נכנס ג'נטלמן לחצר של הבנאי והציע לו מחיר מסוים אם יספק לו מספר עוקב של ערימות מעוקבות אלה, שאמורות להכיל יחד מספר בלוקים שניתן לפרוס ליצירת ריבוע, אך הקונה התעקש על יותר משלוש ערימות וסירב לקחת את הבלוק הבודד מכיוון שהיה בו פגם. מה היה המספר הקטן ביותר האפשרי של בלוקי אבן שהבנאי היה צריך לספק?

    מקורות: