אריתמטיקה

אריתמטיקה היא ענף יסודי במתמטיקה העוסק במספרים ובפעולות הבסיסיות: חיבור, חיסור, כפל וחילוק. שאלות כוללות ביצוע פעולות אלו, הבנת תכונות מספרים (כמו שלמים, שברים, עשרוניים) ופתרון בעיות מילוליות קשורות.

שברים אחוזים חילוק עם שארית

  • מספרי המוניות

    שוטר לונדוני ראה לילה אחד שתי מוניות נוסעות לכיוונים מנוגדים בנסיבות חשודות. השוטר הזה היה אדם זהיר ופקחי במיוחד, והוא הוציא את פנקס הכיס שלו כדי לרשום את מספרי המוניות, אך גילה שהוא איבד את העיפרון שלו. למרבה המזל, עם זאת, הוא מצא חתיכת גיר קטנה, שבעזרתה סימן את שני המספרים על שער הכניסה למזח סמוך. כשחזר לאותו מקום במשמרת שלו, הוא עמד והסתכל שוב על המספרים, והבחין בתכונה המוזרה הזו, שכל תשע הספרות (ללא אפס) היו בשימוש וששום ספרה לא חזרה על עצמה, אבל אם הוא יכפיל את שני המספרים זה בזה, הם ייצרו שוב את תשע הספרות, כולן פעם אחת, ורק פעם אחת. כאשר אחד הפקידים הגיע למזח בשעות הבוקר המוקדמות, הוא הבחין בסימני הגיר ומחק אותם בזהירות. מכיוון שהשוטר לא הצליח להיזכר בהם, התייעצו עם מתמטיקאים מסוימים לגבי קיומה של שיטה ידועה לגילוי כל זוגות המספרים בעלי התכונה המוזרה שהשוטר הבחין בה; אך הם לא הכירו שיטה כזו. עם זאת, החקירה הייתה מעניינת, והשאלה הבאה מתוך רבות הוצעה: אילו שני מספרים, המכילים יחד את כל תשע הספרות, יניבו, כאשר יוכפלו זה בזה, מספר אחר (הגבוה ביותר האפשרי) המכיל גם הוא את כל תשע הספרות? האפס אינו מותר בשום מקום.

    מקורות:

  • כפל מוזר

    אם אני מכפיל `51,249,876` ב-`3` (ובכך משתמש בכל תשע הספרות פעם אחת בלבד), אני מקבל `153,749,628` (שגם הוא מכיל את כל תשע הספרות פעם אחת). באופן דומה, אם אני מכפיל `16,583,742` ב-`9` התוצאה היא `149,253,678`, כאשר בכל מקרה כל תשע הספרות נמצאות בשימוש. כעת, קח `6` כמכפיל שלך ונסה לסדר את שמונה הספרות הנותרות כדי להפיק באמצעות כפל מספר המכיל את כל תשע הספרות פעם אחת בלבד. תגלה שזה לא קל בכלל, אבל אפשר לעשות את זה.
    נושאים:
    אריתמטיקה
    מקורות:

  • חידת תגי המספרים

    במקום בו מועסקים מספר רב של פועלים בבניין, נהוג לספק לכל אדם דיסקית קטנה הנושאת את מספרו. דיסקיות אלו נתלות על לוח על ידי הפועלים כשהם מגיעים, ומשמשות כמעקב אחר דייקנות. פעם שמתי לב שמנהל עבודה הסיר מספר תגים אלה מהלוח שלו והניח אותם על טבעת מפוצלת שנשא בכיסו. זה מיד נתן לי את הרעיון לחידה טובה. למעשה, אני אספר לקוראים שלי שכך בדיוק עולים רעיונות לחידות. אתה לא יכול באמת ליצור רעיון: זה קורה - ואתה צריך להיות בכוננות כדי לתפוס אותו כשזה קורה.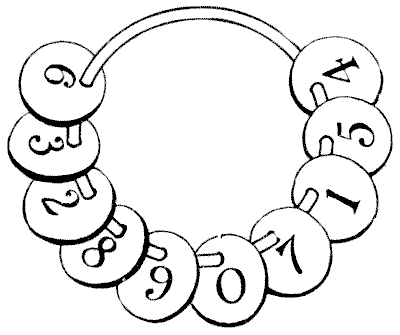 ניתן לראות מהאיור שיש עשרה תגים אלה על טבעת, ממוספרים מ-`1` עד `9` ו-`0`. החידה היא לחלק אותם לשלוש קבוצות מבלי להסיר אף אחד מהם מהטבעת, כך שהקבוצה הראשונה כפול השנייה תיתן את הקבוצה השלישית. לדוגמה, אנו יכולים לחלק אותם לשלוש קבוצות, `2`—`8` `9` `7`—`1` `5` `4` `6` `3`, על ידי הבאת ה-`6` וה-`3` סביב ל-`4`, אבל לצערי שתי הראשונות כשהן מוכפלות יחד לא יוצרות את השלישית. האם אתה יכול להפריד אותם נכון? כמובן שמותר לך שיהיו לך כמה תגים שתרצה בכל קבוצה. החידה דורשת קצת תושייה, אלא אם כן יש לך מזל לפגוע בתשובה במקרה. מקורות:

  • חילוק דיגיטלי

    זוהי חידה טובה נוספת לסדר את תשע הספרות (ללא הספרה אפס) לשתי קבוצות כך שקבוצה אחת, כאשר מחלקים אותה בשנייה, תניב מספר נתון ללא שארית. לדוגמה, `1` `3` `4` `5` `8` חלקי `6` `7` `2` `9` נותן `2`. האם הקורא יכול למצוא סידורים דומים המניבים `3, 4, 5, 6, 7, 8` ו-`9` בהתאמה? כמו כן, האם הוא יכול למצוא את זוגות המספרים הקטנים ביותר האפשריים בכל מקרה? לדוגמה, `1` `4` `6` `5` `8` חלקי `7` `3` `2` `9` נכון באותה מידה עבור `2` כמו הדוגמה האחרת שנתנו, אך המספרים גבוהים יותר. מקורות:

  • חיבור הספרות

    אם ארשום סכום כסף, £`987, 5`s. `4`½d.., ואחבר את הספרות, סכומן הוא `36`. אף ספרה לא נעשה בה שימוש פעם שנייה בסכום או בחיבור. זהו הסכום הגדול ביותר האפשרי בתנאים אלה. כעת מצאו את הסכום הקטן ביותר האפשרי, בלירות, שילינגים, פני ופרטינגים, כאשר כולם מיוצגים. אינכם צריכים להשתמש ביותר מתשע הספרות אם אינכם רוצים, אך אין לחזור על אף ספרה כלל. אסור להשתמש באפס. מקורות:

  • מספרי ריבוע דיגיטליים

    אלה הן תשע הספרות המסודרות כך שהן יוצרות ארבעה מספרי ריבוע: `9, 81, 324, 576`. עכשיו, האם תוכלו לחבר את כולן יחד כדי ליצור מספר ריבוע יחיד - (I) הקטן ביותר האפשרי, ו- (II) הגדול ביותר האפשרי? מקורות:

  • המספר המיסטי אחד עשר

    האם תוכלו למצוא את המספר הגדול ביותר האפשרי המכיל תשע מתוך עשר הספרות (בהתייחסות לאפס כספרה) אשר ניתן לחלק ב-`11` ללא שארית? האם תוכלו למצוא גם את המספר הקטן ביותר האפשרי שנוצר באותו אופן ומתחלק ב-`11`? הנה דוגמה, כאשר הספרה `5` הושמטה: `896743012`. מספר זה מכיל תשע מהספרות ומתחלק ב-`11`, אך הוא אינו המספר הגדול ביותר וגם לא הקטן ביותר שיעבוד.

    מקורות:

  • המאה הדיגיטלית

    `1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9 = 100`.

    נדרש להציב סימנים אריתמטיים בין תשע הספרות כך שהתוצאה תהיה שווה ל- `100`. כמובן, אסור לשנות את הסדר המספרי הקיים של הספרות. האם תוכלו לתת פתרון נכון המשתמש ב- (`1`) מספר הסימנים המועט ביותר האפשרי, וב- (`2`) מספר המינימלי של קווים או נקודות נפרדים של העט? כלומר, יש צורך להשתמש בכמה שפחות סימנים אפשריים, וסימנים אלה צריכים להיות בצורה הפשוטה ביותר. סימני החיבור והכפל (+ ו- ×) ייחשבו כשני קווים, סימן החיסור (-) כקו אחד, סימן החילוק (÷) כשלושה, וכן הלאה.

    מקורות:

  • מספרי הקוביות

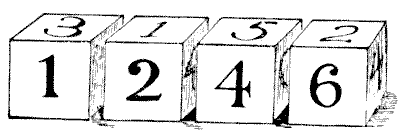
    יש לי סט של ארבע קוביות, שלא מסומנות עם נקודות בצורה רגילה, אלא עם ספרות ערביות, כפי שמוצג באיור. כל קובייה, כמובן, נושאת את המספרים `1` עד `6`. כאשר מצמידים אותן יחד, הן יוצרות מספרים רבים ושונים. כפי שמיוצג, הן מרכיבות את המספר `1246`. עכשיו, אם אני מרכיב את כל המספרים השונים בעלי ארבע ספרות שאפשר ליצור עם הקוביות האלה (אף פעם לא שם את אותה ספרה יותר מפעם אחת באף מספר), לסכום איזה מספר הם יגיעו? מותר לך להפוך את ה-`6` כך שייצג `9`. אני לא מבקש, או מצפה, מהקורא ללכת לכל העבודה של כתיבת הרשימה המלאה של המספרים ואז לחבר אותם. החיים לא ארוכים מספיק בשביל אנרגיה מבוזבזת כזאת. האם אתה יכול להגיע לתשובה בכל דרך אחרת?

    מקורות:

  • שלושים ושלוש הפנינים

    "אדם שאני מכיר," אמר טדי ניקולסון במסיבת משפחה מסוימת, "ברשותו מחרוזת של שלושים ושלוש פנינים. הפנינה האמצעית היא הגדולה והטובה מכולן, והשאר נבחרו וסודרו כך, שמתחילים מקצה אחד, כל פנינה עוקבת שווה £`100` יותר מקודמתה, ישר עד לפנינה הגדולה. מהקצה השני הפנינים עולות בערכן ב-£`150` עד לפנינה הגדולה. כל המחרוזת שווה £`65,000`. מה ערכה של הפנינה הגדולה הזו?"

     

    "פנינים ופריטי לבוש אחרים," אמר הדוד וולטר, כשמחיר הפנינה היקרה התגלה, "מזכירים לי את אדם וחווה. הרשויות, ייתכן שאינכם יודעים, חלוקות לגבי מספר התפוחים שנאכלו על ידי אדם וחווה. יש הסבורים שחווה `8` (אכלה) ואדם `2` (גם), סך הכל `10` בלבד. אבל מתמטיקאים מסוימים חישבו זאת אחרת, וטוענים שחווה `8` ואדם סך הכל `16`. עם זאת, החוקרים האחרונים ביותר חושבים שהמספרים הנ"ל שגויים לחלוטין, כי אם חווה `8` ואדם `82`, הסך הכל חייב להיות `90`."

    "טוב," אמר הארי, "נראה לי שאם היו ענקים בימים ההם, כנראה חווה `81` ואדם `82`, מה שייתן סך של `163`."

    "אני לא מרוצה בכלל," אמרה מוד. "נראה לי שאם חווה `81` ואדם `812`, הם צרכו יחד `893`."

    "אני בטוח שכולכם טועים," התעקש מר וילסון, "כי אני חושב שחווה `814` אדם, ואדם `8124` חווה, אז אנחנו מקבלים סך של `8,938`."

    "אבל, תראו," התפרץ הרברט. "אם חווה `814` אדם ואדם `81242` מחייב את חווה, בטח הסך הכל היה `82,056`!"

    בשלב זה הציע הדוד וולטר שהם יניחו לעניין. הוא הצהיר שזה בבירור מה שמתמטיקאים מכנים בעיה בלתי ניתנת להכרעה.

    מקורות: