אריתמטיקה

אריתמטיקה היא ענף יסודי במתמטיקה העוסק במספרים ובפעולות הבסיסיות: חיבור, חיסור, כפל וחילוק. שאלות כוללות ביצוע פעולות אלו, הבנת תכונות מספרים (כמו שלמים, שברים, עשרוניים) ופתרון בעיות מילוליות קשורות.

שברים אחוזים חילוק עם שארית

  • נשות ההולנדים

    אני תוהה כמה מהקוראים שלי מכירים את החידה של "נשות ההולנדים" —שבה עליכם לקבוע את שמות נשותיהם של שלושה גברים, או, ליתר דיוק, איזו אישה שייכת לכל בעל. לפני כשלושים שנה זה "עבר בין כולם," כמשהו די חדש, אך לאחרונה גיליתי זאת ב-Ladies' Diary עבור `1739-40`, כך שזה היה מוכר בבירור למין היפה לפני יותר ממאה ושבעים שנה. כמה מאמותינו, נשותינו, אחיותינו, בנותינו ודודותינו יוכלו לפתור את החידה היום? נקווה שאחוז גדול בהרבה מאשר אז.

    שלושה הולנדים, בשמות הנדריק, אלס וקורנליוס, ונשותיהם, גורטרון, קטרון ואנה, קונים חזירים. כל אחד קונה כמספר השילינגים שהוא (או היא) נותן עבור אחד. כל בעל משלם בסך הכל שלושה גינאה יותר מאשתו. הנדריק קונה עשרים ושלושה חזירים יותר מקטרון, ואלס אחד-עשר יותר מגורטרון. עכשיו, מה היה שמה של אשת כל גבר?

    מקורות:

  • המתנה לחג המולד של גברת סמיילי

    הבעת ההנאה של גברת סמיילי הייתה כנה כאשר שש נכדותיה שלחו לה, כמתנה לחג המולד, שמיכת טלאים יפה מאוד, שהן הכינו במו ידיהן. היא נבנתה מחתיכות מרובעות של חומר משי, כולן באותו גודל, ומכיוון שהן הכינו שמיכה גדולה עם ארבעה עשר ריבועים קטנים אלה בכל צד, ברור שנתפרו לתוכה בדיוק `196` חתיכות. עכשיו, שש הנכדות תרמו כל אחת חלק מהעבודה בצורה של ריבוע מושלם (כל ששת החלקים בגודל שונה), אך כדי לחבר אותם ליצירת השמיכה המרובעת היה צורך לפרום את עבודתה של ילדה אחת לשלושה חלקים נפרדים. האם תוכלו להראות כיצד ניתן היה לבצע את החיבורים? כמובן, שאף חלק לא ניתן להפוך. מקורות:

  • חידה על עפיפון

    בעודי מלווה את ידידי, פרופסור הייפלייט, בתחרות הטסת עפיפונים מדעית בגבעות הדרומיות של סאסקס, נקלעתי לחישוב קטן שאמור לעניין את קוראיי. הפרופסור פרש את החוט שאליו היה מחובר העפיפון שלו מכננת שעליה הוא גולגל בצורה כדורית לחלוטין. כדור חוט זה היה בדיוק שני רגל בקוטר, ולחוט היה קוטר של מאיות אינץ'. מה היה אורך החוט?

    עכשיו, שאלה קטנה ופשוטה כזו שכולם יכולים להבין לחלוטין תגרום לרבים להתקשות לענות בכל דרך שהיא. בואו נראה אם, מבלי להיכנס לחישובים מתמטיים מעמיקים כלשהם, נוכל לקבל את התשובה בערך - נניח, בטווח של מייל אחד ממה שנכון! נניח שכאשר החוט מגולגל כולו הכדור מוצק לחלוטין לכל אורכו, ואין צורך להתחשב בציר שעובר דרכו. עם הפשטה זו, אני תוהה כמה קוראים יכולים לציין אפילו בטווח של מייל אחד מהתשובה הנכונה את אורך החוט הזה.

    מקורות:

  • שמונה וילות

    באחד מפרבריה החיצוניים של לונדון היה לאיש חלקה מרובעת שעליה החליט לבנות שמונה וילות, כפי שמוצג באיור, עם שטח משחקים משותף באמצע. לאחר שהבתים הושלמו, וכולם או חלקם הושכרו, הוא גילה שמספר הדיירים בשלושת הבתים המרכיבים צד של הריבוע היה בכל מקרה תשעה. הוא לא ציין כיצד הדיירים התפלגו, אבל הראיתי במספרים בצדי הבתים דרך אחת שבה זה יכול היה לקרות. החידה היא לגלות את המספר הכולל של הדרכים שבהן כל הבתים או חלקם יכולים להיות מאוכלסים, כך שיהיו תשעה אנשים בכל צד. כדי שלא יהיו אי הבנות, אסביר שלמרות ש-B הוא מה שאנו מכנים שיקוף של A, אלה ייחשבו כשני הסדרים שונים, בעוד ש-C, אם הוא מסתובב, ייתן ארבעה הסדרים; ואם מסתובבים מול מראה, ארבעה הסדרים אחרים. יש לספור את כל שמונתם. מקורות:

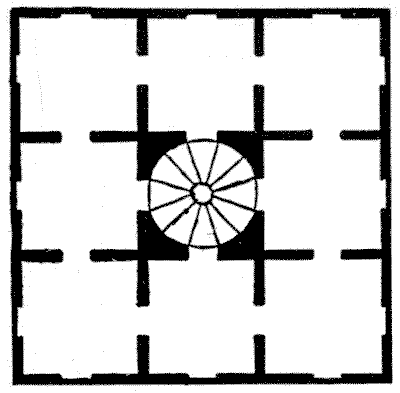
  • חידת מעונות

    במנזר מסוים היו שמונה מעונות גדולים בקומה אחת, שאליהם הגיעה גרם מדרגות ספירלי במרכז, כפי שמוצג בתרשים שלנו. בבדיקה שערכה אם המנזר ביום שני אחד, התגלה שהצד הדרומי מועדף כל כך, שפי שישה נזירות ישנו בצד הדרומי מאשר בכל אחד משלושת הצדדים האחרים. היא התנגדה לצפיפות היתר הזו, והורתה לצמצם אותה. ביום שלישי היא גילתה שפי חמש נזירות ישנו בצד הדרומי מאשר בכל אחד מהצדדים האחרים. שוב היא התלוננה. ביום רביעי היא מצאה פי ארבעה בצד הדרומי, ביום חמישי פי שלושה, וביום שישי פי שניים. לאחר שהאיצה בנזירות להמשיך במאמצים, היא שמחה לגלות ביום שבת שמספר שווה ישן בכל אחד מארבעת צדי הבית. מהו המספר הקטן ביותר של נזירות שיכול היה להיות שם, וכיצד הן יכלו להסתדר בכל אחד מששת הלילות? אסור שאף חדר יהיה ריק.

    מקורות:

  • ערבוב התה

    "גברת ספונר התקשרה הבוקר," אמר המכולת הישר לעוזרו. "היא רוצה עשרים ליברות של תה ב-`2`s. `4`½d. לליברה. כמובן שיש לנו תה טוב ב-`2`s. `6`d., מעט נחות יותר ב-`2`s. `3`d., ותה הודי זול ב-`1`s. `9`d., אבל היא מאוד ספציפית תמיד לגבי המחירים שלה."

    "מה אתה מציע לעשות?" שאל העוזר התמים.

    "לעשות?" קרא המכולת. "פשוט לערבב את שלושת סוגי התה בפרופורציות שונות, כך שעשרים הליברות יסתדרו בצורה הוגנת במחיר של הגברת. רק אל תשים יותר מדי מהתה הטוב ביותר כפי שתוכל, מכיוון שאנחנו מרוויחים פחות על זה, וכמובן שתשתמש רק בחבילות הפאונד השלמות שלנו. אל תעשה שום שקילה."

    כיצד היה העוזר המסכן אמור לערבב את שלושת סוגי התה? האם היית יכול להראות לו איך לעשות זאת?

    מקורות:

  • פאזל אריזה

    כפי שכולנו יודעים מניסיון, לעתים קרובות נדרשת תושייה רבה באריזת חפצים לקופסה, אם לא רוצים לבזבז מקום שלא לצורך. אדם סיפר לי פעם שהיו לו מספר רב של כדורי ברזל, שקוטרם בדיוק שני אינץ' כל אחד, והוא רצה לארוז כמה שיותר מהם לתוך קופסה מלבנית באורך `24` `9/10` אינץ', ברוחב `22` `4/5` אינץ' ובעומק `14` אינץ'. מהו המספר הגדול ביותר של כדורים שהוא יכול לארוז בקופסה הזו? מקורות:

  • אריזת זהב ברוסיה

    עורך העיתון Times הוזמן על ידי פקיד רוסי בכיר לבדוק את הזהב המאוחסן במאגר בסנט פטרסבורג, כדי שיוכל לוודא שזה לא עוד "כספת הומברט". הוא השיב שזה לא יועיל כלל, כי למרות שהזהב עשוי להיראות שם, הוא לא יוכל מתוך בדיקה בלבד להצהיר שמה שהוא רואה הוא באמת זהב. כתב של ה-Daily Mail הרים את הכפפה, אך למרות שהתרשם מאוד ממה שראה, הוא נאלץ להודות בחוסר יכולתו (מבלי לרוקן ולספור את תכולת כל קופסה ושק, ולבדוק כל חתיכת זהב) לתת כל הבטחה בנושא. בהצגת החידה הקטנה הבאה, אני רוצה שיהיה מובן גם שאני לא מבטיח את קיומו האמיתי של הזהב, והנקודה כלל לא מהותית למטרתנו. יתר על כן, אם הקורא יאמר שבדרך כלל לא "אורזים" זהב בלוחות במידות שאני נותן, אני יכול רק לטעון לרישיון בעייתי.

    פקידים רוסים עסקו באריזת `800` לוחות זהב, שכל אחד מהם באורך `12`½ אינץ', ברוחב `11` אינץ' ובעומק `1` אינץ'. מהם הממדים הפנימיים של קופסה באורך וברוחב שווים, ועומק נדרש, שתכיל אותם בדיוק מבלי להשאיר מקום פנוי? לא יותר משנים עשר לוחות ניתן להניח על קצה, על פי כללי הממשלה. זוהי בעיה קטנה ומעניינת באריזה, וכלל לא קשה.

    מקורות:

  • פאזל מסגרת הדומינו

    ניתן לראות באיור שהסט המלא של עשרים ושמונה אבני הדומינו מסודר בצורת מסגרת מרובעת, כאשר `6` מול `6, 2` מול `2`, ריק מול ריק, וכן הלאה, כמו במשחק. יתגלה כי הנקודות בשורה העליונה ובטור השמאלי מסתכמות ל-`44`. הנקודות בשני הצדדים האחרים מסתכמות ל-`59` ו-`32` בהתאמה. הפאזל הוא לסדר מחדש את אבני הדומינו באותה צורה כך שכל ארבעת הצדדים יסתכמו ל-`44`. זכור שאבני הדומינו חייבות להיות מונחות נכון אחת מול השנייה כמו במשחק. מקורות:

  • פאזל מסגרת הקלפים

    באיור יש לנו מסגרת הבנויה מעשרה קלפי משחק, אס עד עשר יהלום. הילדים שהכינו אותה רצו שהנקודות ניקוד בכל ארבעת הצדדים יסתכמו באופן שווה, אבל הם נכשלו בניסיונם וויתרו עליה כבלתי אפשרית. ניתן לראות שהנקודות בשורה העליונה, בשורה התחתונה ובצד שמאל מסתכמות כולן ב-`14`, אבל הצד הימני מסתכם ב-`23`. עכשיו, מה שהם ניסו לעשות הוא די אפשרי. האם אתה יכול לסדר מחדש את עשרת הקלפים באותה תצורה כך שכל ארבעת הצדדים יסתכמו באופן שווה? כמובן שהם לא צריכים להסתכם ב-`14`, אלא בכל מספר שתבחר.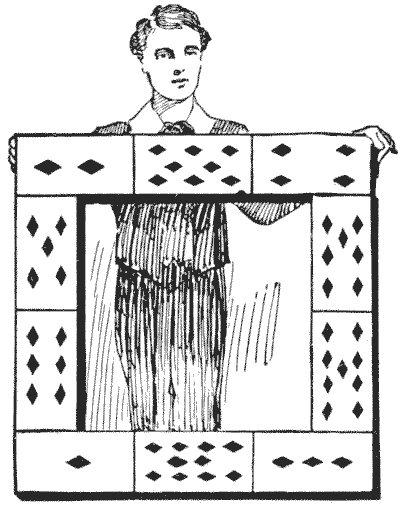 מקורות: