גאומטריה, גאומטריה במישור

גאומטריה במישור עוסקת בצורות וגופים על משטח שטוח ודו-ממדי. היא מכסה תכונות של נקודות, קווים, זוויות, מצולעים (כמו משולשים ומרובעים) ומעגלים. שאלות כוללות בדרך כלל הוכחות, בנייה וחישובים הקשורים לאלמנטים אלו.

חשבון שטחים משולשים מעגלים סימטריה חשבון זוויות משפט פיתגורס אי שוויון המשולש

• שאלה

  לשלומי יש קופסה שטוחה בגודל `5xx5` סנטימטרים. שלומי טוען, שכל מלבן שאפשר לאחסן בקופסה הזאת, כל צלעותיו צריכות להיות קטנות מ-5 סנטימטרים. האם הוא צודק?

  נושאים:

  הוכחה ודוגמה -> בניית דוגמה גאומטריה -> גאומטריה במישור -> משפט פיתגורס

• שאלה

  נתון מגדל בצורת תיבה. גובהו 61 מטרים, ובסיסו הוא ריבוע שצלעו 9 מטרים. על הגג,
  בנקודה שנמצאת במרחק של שני מטרים מהקיר הצפוני ושני מטרים מהקיר המערבי, שפכו
  מיץ. נמלה נמצאת בתחתית המגדל, בפינה הדרום מזרחית. לנמלה יש חוש ריח מעולה ולכן
  היא מרגישה איפה בדיוק נשפך המיץ. מהו המרחק המינימלי שהיא צריכה לעבור בשביל
  להגיע לנקודה הזאת? (הנמלה יכול לזחול על הקירות והגג.)
  נושאים:

  גאומטריה -> גאומטריה במרחב גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • מבחני בחירה ל-IMO בישראל, תשע"ב, שלב א שאלה 9

• בעיה נוספת של נגר

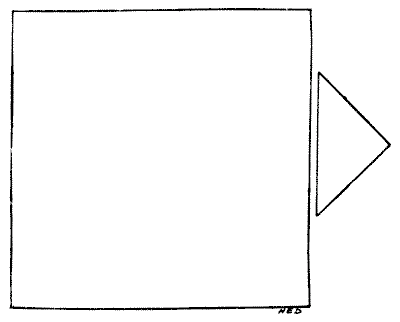  לנגר היו שני חתיכות עץ בצורות ובפרופורציות יחסיות המוצגות בדיאגרמה. הוא רצה לחתוך אותן למספר קטן ככל האפשר של חלקים כך שניתן יהיה לחבר אותם יחד, ללא בזבוז, וליצור משטח שולחן מרובע לחלוטין. איך הוא היה צריך לעשות את זה? אין צורך לתת מידות, כי אם החלק הקטן יותר (שהוא חצי ריבוע) יהיה קצת גדול מדי או קטן מדי, זה לא ישפיע על שיטת הפתרון.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 152

• ריבוע הפורניר

  הבא מייצג חתיכת עץ ברשותי, `5` אינץ' מרובע. על ידי סימונים על פני השטח הוא מחולק לעשרים וחמישה אינצ'ים מרובעים. אני רוצה לגלות דרך לחתוך את חתיכת העץ הזו למספר המינימלי האפשרי של חלקים שיתאימו יחד וייצרו שני ריבועים מושלמים בגדלים שונים ובמידות ידועות. אבל, לצערי, בכל אחד משש עשרה הצמתים של קווי החיתוך נתקע מסמר קטן מתישהו, והמסור הנימי שלי ייפגע אם הוא יבוא במגע עם אחד מאלה. לכן אני צריך למצוא שיטה לעשות את העבודה שלא תחייב אותי לחתוך דרך אף אחת משש עשרה הנקודות האלה. איך זה אמור להיעשות? זכור, יש לתת את המידות המדויקות של שני הריבועים.
  נושאים:

  גאומטריה -> חשבון שטחים אלגברה גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 159

• חיתוך לינולאום

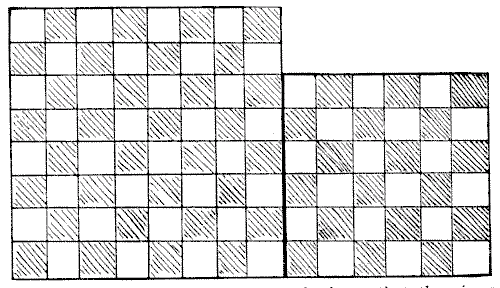  הדיאגרמה כאן מייצגת שני חלקי לינולאום נפרדים. דוגמת המשבצות לא חוזרת על עצמה בגב, כך שלא ניתן להפוך את החלקים. החידה היא לחתוך את שתי הריבועים לארבעה חלקים כך שהם יתאימו זה לזה וייצרו ריבוע מושלם אחד בגודל `10`×`10`, כך שהדוגמה תתאים כראוי, וכך שלחלק הגדול יותר יהיה חלק קטן ככל האפשר שנחתך ממנו.
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> משפט פיתגורס קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 176

• גְּנֵבַת חַבְלֵי הַפַּעֲמוֹנִים

  שְׁנֵי אֲנָשִׁים פָּרְצוּ לְמִגְדַּל כְּנֵסִיָּה לַיְלָה אֶחָד כְּדֵי לִגְנֹב אֶת חַבְלֵי הַפַּעֲמוֹנִים. שְׁנֵי הַחֲבָלִים עָבְרוּ דֶּרֶךְ חֹרִים בַּתִּקְרָה הָעֲשׂוּיָה עֵץ שֶׁהָיְתָה מֵעֲלֵיהֶם, וְהֵם לֹא בִּזְבְּזוּ זְמַן וְטִפְּסוּ לְרֹאשׁ הַמִּגְדָּל. אָז אִישׁ אֶחָד שָׁלַף אֶת סַכִּינוֹ וְחָתַךְ אֶת הַחֶבֶל מֵעַל רֹאשׁוֹ, וּכְתוֹצָה מִכָּךְ הוּא נָפַל עַל הָרִצְפָּה וְנִפְצַע קָשׁוֹת. חֲבֵרוֹ-הַגַּנָּב קָרָא שֶׁמַּגִּיעַ לוֹ עַל שֶׁהוּא כָּזֶה טִפֵּשׁ. הוּא אָמַר שֶׁהוּא הָיָה צָרִיךְ לַעֲשׂוֹת כְּפִי שֶׁהוּא עוֹשֶׂה, וְעַל כֵּן הוּא חָתַךְ אֶת הַחֶבֶל מִתַּחַת לַמָּקוֹם שֶׁבּוֹ הוּא הֶחְזִיק. אָז, לְתַדְהֵמָתוֹ, הוּא גִּלָּה שֶׁהוּא לֹא בְּמַצָּב טוֹב יוֹתֵר, כִּי אַחֲרֵי שֶׁנִּתְלָה כָּל עוֹד כֹּחוֹ הֶחְזִיק מַעֲמָד, הוּא הֻכְרַח לְהַרְפּוֹת וְלִנְפֹּל לְצַד חֲבֵרוֹ. כָּאן שְׁנֵיהֶם נִמְצְאוּ לְמָחֳרָת בַּבֹּקֶר עִם גְּפָפִים שְׁבוּרִים. מָה הָיָה גֹּבַהּ הַנְּפִילָה שֶׁלָּהֶם? אֶחָד מֵהַחֲבָלִים, כְּשֶׁמָּצְאוּ אוֹתוֹ, רַק נָגַע בָּרִצְפָּה, וְכַאֲשֶׁר מָשַׁכְתָּ אֶת הַקָּצֶה אֶל הַקִּיר, כְּשֶׁהַחֶבֶל מָתוּחַ, הוּא נָגַע בְּנְקֻדָּה שֶׁהִיא רַק שְׁלוֹשָׁה אִינְטְשִׁים מֵעַל הָרִצְפָּה, וְהַקִּיר הָיָה אַרְבָּעָה רֶגֶלִים מֵהַחֶבֶל כְּשֶׁהוּא תָּלוּי בְּמָנוֹחַ. מָה הָאֹרֶךְ שֶׁל הַחֶבֶל מֵהָרִצְפָּה עַד הַתִּקְרָה?
  נושאים:

  אלגברה גאומטריה -> גאומטריה במישור -> משפט פיתגורס
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 179

• שאלה

  במרחב נתונים 30 וקטורים לא מנוונים. הוכח כי יש לפחות 2 שהזווית ביניהם היא לא גדולה מ- 45 מעלות. 
  א. טולפיגו

  נושאים:

  גאומטריה -> טריגונומטריה גאומטריה -> גאומטריה על כדור קומבינטוריקה -> עקרון שובך היונים קומבינטוריקה -> גאומטריה קומבינטורית גאומטריה -> גאומטריה במישור -> חשבון זוויות גאומטריה -> ווקטורים
  מקורות:
  • תחרות הערים, תש"מ, עיקרית, אביב שאלה 4

• 5 מעלות בשעון

  באיזה שעה יש זווית 5 מעלות בין מחוגי השעון?

  נושאים:

  גאומטריה -> גאומטריה במישור -> חשבון זוויות
  מקורות:
  • אולימפיאדת בנו ארבל, 2013, כיתה ז שאלה 5

• שאלה

  האם קיים מרובע קמור שכל אחד מהאלכסונים שלו מחלק אותו לשני משולשים חדי זוויות?

  נושאים:

  הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במישור -> חשבון זוויות

• מחוגים מאונכים

  מספר פעמים ביממה מחוג השעות ומחוג הדקות נמצאים על ישר אחד ויוצרים זווית של `180^@`. האם בין כל הישרים האלה יש ישרים שמאונכים זה לזה?

  נושאים:

  לוגיקה הוכחה ודוגמה -> הוכחה בשלילה גאומטריה -> גאומטריה במישור -> חשבון זוויות