גאומטריה, גאומטריה במישור

גאומטריה במישור עוסקת בצורות וגופים על משטח שטוח ודו-ממדי. היא מכסה תכונות של נקודות, קווים, זוויות, מצולעים (כמו משולשים ומרובעים) ומעגלים. שאלות כוללות בדרך כלל הוכחות, בנייה וחישובים הקשורים לאלמנטים אלו.

חשבון שטחים משולשים מעגלים סימטריה חשבון זוויות משפט פיתגורס אי שוויון המשולש

• שאלה

  ידוע כי כל הזוויות של הצורה הנתונה ישרות. חתכו את הצורה לשני מצולעים שווי שטח. מותר להיעזר רק בסרגל ללא שנתות.

  

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה

• שטח אפור

  בציור מלבן המורכב מ-5 ריבועים בגודל `2 times 2 ` וישר שחוצה אותו באלכסון.
  מצאו את השטח המושחר.

  

  נושאים:

  גאומטריה -> חשבון שטחים גאומטריה -> גאומטריה במישור -> סימטריה
  מקורות:
  • האולימפיאדה לצעירים, תשע"ט, שלב א, כיתות ג-ד שאלה 3

• שאלה

  בקודקודיו של מחומש משוכלל כתובים המספרים `1,2,3,4,5`, כל מספר בקודקוד אחד בדיוק. שלשה של קודקודים נקראת מוצלחת אם היא יוצרת משולש שווה שוקיים, שבקודקוד הראש שלו יש מספר גדול יותר מבשני הקודקודים האחרים או שבקודקוד הראש שלו יש מספר קטן יותר מבשני הקודקודים האחרים.

  מצאו את המספר המרבי של שלשות מוצלחות שיכולות להיות.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  הוכחה ודוגמה -> בניית דוגמה קומבינטוריקה -> בדיקת מקרים -> תהליכים גאומטריה -> גאומטריה במישור -> סימטריה בעיות מינימום ומקסימום

• לחתוך לארבעה חלקים

  צורות גיאומטריות נקראות חופפות אם הן מתלכדות כאשר שמים אותן זו על זו.חתכו את הצורה הבאה לארבעה חלקים חופפים:

  

  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה גאומטריה -> גאומטריה במישור -> העתקות של מישור -> העתקות חפיפה (איזומטריות)
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ג-ד שאלה 3

• חתכו סירה לשניים

  צורות גיאומטריות נקראות חופפות אם הן מתלכדות כאשר שמים אותן זו על זו. חתכו את הצורה לשני חלקים חופפים

  

  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • האולימפיאדה לצעירים, תש"פ, גמר, כיתות ה-ו שאלה 6

• איפה הנקודה?

  במשושה קמור ABCDEF המשולשים
  ACE ו-BDF משוכללים וחופפים. הראו כי
  שלושת הקטעים המחברים את אמצעי
  הצלעות הנגדיות של המשושה נחתכים
  בנקודה אחת.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה גאומטריה -> גאומטריה במישור -> משולשים -> חפיפת משולשים גאומטריה -> ווקטורים
  מקורות:
  • אולימפיאדת גיליס, תש"פ שאלה 3

• הפודינג של חג המולד

  "אם כבר מדברים על פודינגים של חג המולד," אמר המארח, כשהוא מביט במעדן המרשים בקצה השני של השולחן. "זה מזכיר לי את העובדה שידיד נתן לי חידה חדשה אתמול בנוגע לאחד כזה. הנה זה," הוא הוסיף, כשהוא צולל לתוך כיס חזה שלו.

  "'הבעיה: למצוא את התכולה,' אני מניח," אמר הנער מאיטון.

  "לא; ההוכחה לכך היא באכילה. אני אקריא לכם את התנאים."

   

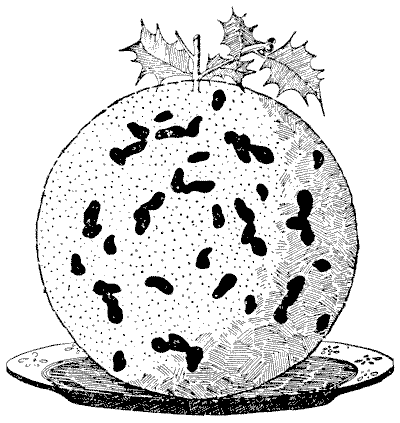
  "'חתכו את הפודינג לשני חלקים, כל אחד בדיוק באותו גודל וצורה, מבלי לגעת באף אחד מהשזיפים. יש להתייחס לפודינג כאל דיסקה שטוחה, לא כאל כדור.'"

  "למה אתה צריך להתייחס לפודינג חג המולד כדיסקה? ומדוע שאדם הגיוני כלשהו ירצה אי פעם לעשות חלוקה מדויקת כזו?" שאל הציניקן.

  "זו רק חידה—בעיה בדיסקציה." כולם בתורם הסתכלו על החידה, אבל אף אחד לא הצליח לפתור אותה. זה קצת קשה אלא אם כן אתה מכיר את העיקרון הכרוך בהכנת פודינגים כאלה, אבל קל מספיק כשאתה יודע איך זה נעשה.

  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 168

• לוחות עם מספר אי-זוגי של משבצות

  אנו נדון כאן בשאלה של אותם לוחות המכילים מספר אי-זוגי של משבצות. נניח שהמשבצת המרכזית נחתכת תחילה, כך שיישאר מספר זוגי של משבצות לחלוקה. כעת, ברור שלוח ריבוע שלוש על שלוש ניתן לחלוקה רק בדרך אחת, כפי שמוצג באיור `1`. ניתן לראות שהחלקים A ו-B הם באותו גודל וצורה, וכי כל דרך חיתוך אחרת תייצר רק חלקים בעלי צורה זהה, אז זכרו שווריאציות אלה אינן נספרות כדרכים שונות. החידה שאני מציע היא לחתוך את הלוח חמש על חמש (איור `2`) לשני חלקים באותו גודל וצורה בכמה שיותר דרכים שונות. הדגמתי באיור דרך אחת לעשות זאת. כמה דרכים שונות יש בסך הכל? חתיכה שכאשר הופכים אותה דומה לחתיכה אחרת אינה נחשבת כבעלת צורה שונה.
  נושאים:

  גאומטריה -> גאומטריה במישור -> סימטריה קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה קומבינטוריקה -> גאומטריה קומבינטורית -> גאומטריה על נייר משבצות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 290

• חידת הסיגר

  הצעתי פעם את החידה הבאה במועדון לונדוני, ולתקופה ניכרת היא ספגה את תשומת הלב של החברים. הם לא הצליחו להבין אותה, וחשבו שהיא בלתי אפשרית לפתרון. ובכל זאת, כפי שאראה, התשובה פשוטה להפליא.

  שני אנשים יושבים ליד שולחן מרובע. אחד מניח סיגר רגיל (שטוח בקצה אחד, מחודד בקצה השני) על השולחן, ואז השני עושה את אותו הדבר, וכן הלאה לסירוגין, בתנאי שאף סיגר לא יגע באחר. איזה שחקן יצליח להניח את הסיגר האחרון, בהנחה שכל אחד מהם ישחק בצורה הטובה ביותר האפשרית? גודל פני השולחן וגודל הסיגר אינם נתונים, אך כדי לשלול את התשובה המגוחכת שהשולחן עשוי להיות כה קטן עד שהוא יכול להכיל רק סיגר אחד, נאמר שהשולחן לא יהיה קטן מ- `2` רגל מרובע והסיגר לא יותר מ- `4`½ אינץ' אורך. עם ההגבלות האלה אתה יכול לקחת כל מימד שתרצה. כמובן שאנו מניחים שכל הסיגרים זהים לחלוטין בכל מובן. האם השחקן הראשון או השחקן השני ינצח?

  נושאים:

  קומבינטוריקה -> תורת המשחקים לוגיקה -> הגיון גאומטריה -> גאומטריה במישור -> סימטריה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 398

• שאלה

  נתון חרוט (בעל ציר סימטריה במרכזו, המאונך לבסיסו) שגובהו 6 ובסיסו הוא עיגול בעל רדיוס `sqrt2` . בתוך החרוט חסומה קובייה – היא מונחת על בסיס החרוט וכל קדקודיה העליונים נוגעים בחרוט. מצאו את אורך הצלע של הקובייה. נמקו את תשובתכם.

  

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
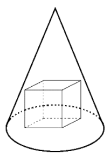  נושאים:

  גאומטריה -> גאומטריה במרחב אלגברה -> משוואות גאומטריה -> גאומטריה במישור -> משפט פיתגורס גאומטריה -> גאומטריה במישור -> משולשים -> דמיון משולשים
  מקורות:
  • אולימפיאדת גיליס, תשע"ו שאלה 2