אלגברה, משוואות

משוואה היא טענה ששני ביטויים מתמטיים שווים. פתרון משוואה כולל מציאת ערכי המשתנים שהופכים את הטענה לאמיתית. שאלות מכסות סוגים שונים: לינאריות, ריבועיות, פולינומיאליות, רציונליות, רדיקליות ומערכות משוואות.

משוואות דיופנטיות

  • ההפסד הקטן של ראקבריין

    הפרופסור ראקבריין בילה ערב עם חבריו הוותיקים, מר וגברת פוטס, והם שיחקו במשחק כלשהו (הוא לא מציין איזה משחק) קלפים. הפרופסור הפסיד במשחק הראשון, מה שהביא להכפלת הכסף שהונח על השולחן על ידי מר וגברת פוטס. את המשחק השני הפסידה גברת פוטס, מה שהכפיל את הכסף שהיה אז לבעלה ולפרופסור. באופן מוזר למדי, את המשחק השלישי הפסיד מר פוטס, והייתה לכך השפעה של הכפלת הכסף שהיה אז לאשתו ולפרופסור. לאחר מכן התברר שלכל אחד מהם היה בדיוק אותו סכום כסף, אך הפרופסור הפסיד חמישה שילינגים במהלך המשחק. כעת, שואל הפרופסור, מה היה סכום הכסף איתו הוא התיישב לשולחן? האם תוכלו לומר לו? מקורות:

  • החקלאי והכבשים שלו

     

    לחקלאי לונגמור הייתה נטייה מוזרה לחשבון, והוא היה ידוע באזורו כ"חקלאי המתמטי". הכומר החדש לא היה מודע לעובדה זו כשפגש את אחד מבני קהילתו בדרך, ושאל אותו במהלך שיחה קצרה, "ובכן, כמה כבשים יש לך בסך הכל?" לכן הוא הופתע למדי מתשובתו של לונגמור, שהייתה כדלקמן: "אתה יכול לחלק את הכבשים שלי לשני חלקים שונים, כך שההפרש בין שני המספרים יהיה זהה להפרש בין הריבועים שלהם. אולי, כבוד הכומר, תרצה לפתור את הסכום הקטן בעצמך."

    האם הקורא יכול לומר בדיוק כמה כבשים היו לחקלאי? נניח שהיו לו רק עשרים כבשים, והוא חילק אותן לשני החלקים `12` ו-`8`. עכשיו, ההפרש בין הריבועים שלהם, `144` ו-`64`, הוא `80`. אז זה לא יתאים, כי `4` ו-`80` בהחלט לא זהים. אם אתה יכול למצוא מספרים שמסתדרים נכון, תדע בדיוק כמה כבשים היו בבעלותו של החקלאי לונגמור.

    מקורות:

  • חידת הנדנדה

    הצורך הוא אכן אם ההמצאה. נהניתי מאוד אתמול כשצפיתי בילד שרצה לשחק בנדנדה, ובשל כישלונו למצוא ילד אחר שיחלוק איתו את המשחק, הוא נאלץ לחזור אל הפתרון הגאוני של קשירת מספר לבנים לקצה אחד של הקרש כדי לאזן את משקלו בקצה השני.

    למעשה, הוא בדיוק התאזן מול שש-עשרה לבנים, כאשר אלה היו מחוברות לקצה הקצר של הקרש, אבל אם הוא חיבר אותן לקצה הארוך של הקרש הוא היה צריך רק אחת-עשרה לבנים כדי להתאזן.

    עכשיו, מה היה משקלו של הילד, אם לבנה שוקלת משקל שווה לשלושה רבעים של לבנה ושלושה רבעים של פאונד?

    מקורות:

  • הדילמה של אנשי הארטילריה

    "יש לערום את כל כדורי התותח בפירמידות מרובעות," הייתה הפקודה שהוצאה לגדוד. כך נעשה. ואז הגיעה הפקודה הנוספת, "כל הפירמידות צריכות להכיל מספר ריבועי של כדורים." ואז החלו הצרות. "אי אפשר לעשות את זה," אמר המג'ור. "תסתכלו על הפירמידה הזו, למשל; יש שישה עשר כדורים בבסיס, אחר כך תשעה, אחר כך ארבעה, ואז אחד בקצה, מה שנותן שלושים כדורים בסך הכל. אבל חייבים להיות עוד שישה כדורים, או חמישה פחות, כדי ליצור מספר ריבועי." "חייבים לעשות את זה," התעקש הגנרל. "כל מה שאתם צריכים לעשות הוא לשים את המספר הנכון של כדורים בפירמידות שלכם." "הבנתי!" אמר סגן, הגאון המתמטי של הגדוד. "הניחו את הכדורים בנפרד." "שטויות!" קרא הגנרל. "אתה לא יכול לערם כדור אחד לפירמידה!" האם באמת אפשר לציית לשתי הפקודות? מקורות:

  • קופסת הקרטון

    חידה זו אינה קשה, אך יהיה משעשע לגלות את הכלל הפשוט לפתרונה. יש לי קופסת קרטון מלבנית. לשטח החלק העליון `120` אינץ' רבוע, לשטח הצד `96` אינץ' רבוע, ולשטח הקצה `80` אינץ' רבוע. מהם הממדים המדויקים של הקופסה? מקורות:

  • חידת הגינה

    פרופסור רַאקְבְּרֵיין סיפר לי שעישן לאחרונה מקטרת ידידותית מתחת לעץ בגינה של מכר כפרי. הגינה הייתה מוקפת בארבעה קירות ישרים, וידידו הודיע לו שהוא מדד אותם ומצא שאורכם הוא `80, 45, 100`, ו-`63` יארד בהתאמה. "אם כך," אמר הפרופסור, "נוכל לחשב את השטח המדויק של הגינה." "זה בלתי אפשרי," השיב המארח שלו, "כי אתה יכול לקבל מספר אינסופי של צורות שונות עם ארבעת הצדדים האלה." "אבל אתה שוכח," אמר רַאקְבְּרֵיין, עם ניצוץ בעיניו, "שאמרת לי פעם ששתלת את העץ הזה במרחק שווה מכל ארבע פינות הגינה." האם תוכלו לחשב את שטח הגינה? מקורות:

  • חידת חבל הכביסה

    ילד קשר חבל כביסה מראש כל אחד משני עמודים לבסיס של השני. לאחר מכן הוא הציע לאביו את השאלה הבאה. אם עמוד אחד היה בדיוק שבעה רגל מעל הקרקע והשני בדיוק חמישה רגל, מה היה הגובה מהקרקע שבו שני החבלים הצטלבו זה בזה? מקורות:

  • חידת הירח

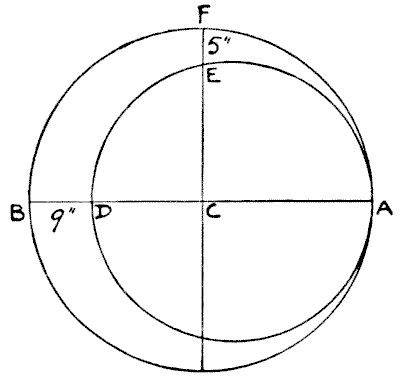    הנה חידה גיאומטרית קלה. הירח נוצר על ידי שני מעגלים, ו-C הוא מרכז המעגל הגדול יותר. רוחב הירח בין B ל-D הוא `9` אינץ', ובין E ל-F הוא `5` אינץ'. מהם הקטרים של שני המעגלים? מקורות:

  • הגן של ליידי בלינדה

    ליידי בלינדה היא גננת נלהבת. באיור היא מתוארת כשהיא שקועה בפתרון בעיה קטנה ומהנה שאותה אספר. אחד הגנים שלה הוא בצורת מלבן, מוקף בגדר חיה גבוהה של צמח ההולי, והיא הופכת אותו לגינת ורדים לטיפוח כמה מזני הורדים המשובחים ביותר שלה. היא רוצה להקדיש בדיוק מחצית משטח הגן לפרחים, בערוגה גדולה אחת, ואת המחצית השנייה לשביל המקיף אותו מכל צדדיו ברוחב שווה. גן כזה מוצג בתרשים בתחתית התמונה. כיצד עליה לסמן את הגן בתנאים פשוטים אלה? יש לה רק סרט מדידה, באורך הגן, כדי לעשות זאת, ומכיוון שגדר ההולי עבה וצפופה מאוד, עליה לבצע את כל המדידות בפנים. ליידי בלינדה לא ידעה את המידות המדויקות של הגן, ומכיוון שלא היה צורך שתדע, גם אני לא מציין מידות. זו משימה פשוטה למדי, לא משנה מה גודל או פרופורציות הגן. עם זאת, כמה גננות היו יודעות בדיוק כיצד להמשיך? סרט המדידה יכול להיות פשוט למדי - כלומר, אין צורך שיהיה מדד מדורג. מקורות:

  • חבית היין

    הנה בעיה קטנה ומסקרנת. לאיש הייתה חבית בת עשרה גלונים מלאה ביין וכד. יום אחד הוא שאב כד מלא ביין ומילא את החבית במים. לאחר מכן, כאשר היין והמים התערבבו היטב, הוא שאב כד נוסף ומילא שוב את החבית במים. אז התגלה כי החבית הכילה כמויות שוות של יין ומים. האם תוכלו למצוא מנתונים אלה את נפח הכד? מקורות: