אלגברה, משוואות

משוואה היא טענה ששני ביטויים מתמטיים שווים. פתרון משוואה כולל מציאת ערכי המשתנים שהופכים את הטענה לאמיתית. שאלות מכסות סוגים שונים: לינאריות, ריבועיות, פולינומיאליות, רציונליות, רדיקליות ומערכות משוואות.

• ערבוב התה

  "גברת ספונר התקשרה הבוקר," אמר המכולת הישר לעוזרו. "היא רוצה עשרים ליברות של תה ב-`2`s. `4`½d. לליברה. כמובן שיש לנו תה טוב ב-`2`s. `6`d., מעט נחות יותר ב-`2`s. `3`d., ותה הודי זול ב-`1`s. `9`d., אבל היא מאוד ספציפית תמיד לגבי המחירים שלה."

  "מה אתה מציע לעשות?" שאל העוזר התמים.

  "לעשות?" קרא המכולת. "פשוט לערבב את שלושת סוגי התה בפרופורציות שונות, כך שעשרים הליברות יסתדרו בצורה הוגנת במחיר של הגברת. רק אל תשים יותר מדי מהתה הטוב ביותר כפי שתוכל, מכיוון שאנחנו מרוויחים פחות על זה, וכמובן שתשתמש רק בחבילות הפאונד השלמות שלנו. אל תעשה שום שקילה."

  כיצד היה העוזר המסכן אמור לערבב את שלושת סוגי התה? האם היית יכול להראות לו איך לעשות זאת?

  נושאים:

  אריתמטיקה אלגברה -> משוואות אלגברה -> בעיות מילוליות יחידות מידה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 369

• פאזל מסגרת הקלפים

  באיור יש לנו מסגרת הבנויה מעשרה קלפי משחק, אס עד עשר יהלום. הילדים שהכינו אותה רצו שהנקודות ניקוד בכל ארבעת הצדדים יסתכמו באופן שווה, אבל הם נכשלו בניסיונם וויתרו עליה כבלתי אפשרית. ניתן לראות שהנקודות בשורה העליונה, בשורה התחתונה ובצד שמאל מסתכמות כולן ב-`14`, אבל הצד הימני מסתכם ב-`23`. עכשיו, מה שהם ניסו לעשות הוא די אפשרי. האם אתה יכול לסדר מחדש את עשרת הקלפים באותה תצורה כך שכל ארבעת הצדדים יסתכמו באופן שווה? כמובן שהם לא צריכים להסתכם ב-`14`, אלא בכל מספר שתבחר.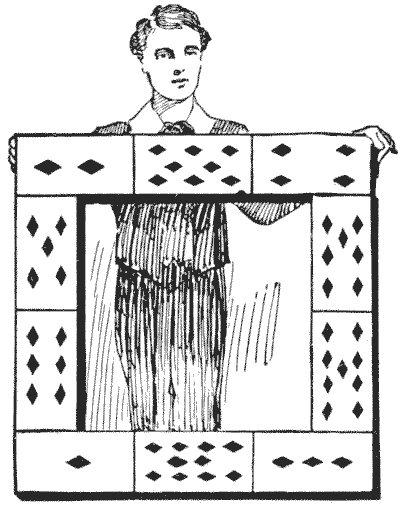
  נושאים:

  אריתמטיקה אלגברה -> משוואות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 381

• חידת מרוץ הסוסים

  אין מוסר בחידות. כאשר אנו פותרים את החידה הישנה על הקברניט שנאלץ להשליך חצי מצוותו מעבר לסיפון בסערה, והסכים לערוך הגרלה, אך סידר את האנשים כך שרק הטורקים הוקרבו, וכל הנוצרים נותרו על הסיפון, איננו עוצרים לדון במוסריות המפוקפקת של ההליך. וכאשר אנו עוסקים בבעיית מדידה, שבה צליינים צמאים מסוימים אמורים לערוך חלוקה הוגנת של חבית בירה, איננו מתנגדים לכך, כמנועים מוחלטים, שזה מנוגד למצפוננו להתעסק עם משקאות משכרים. לכן איני מתנצל על הצגת חידה העוסקת בהימורים.

  שלושה סוסים—בלוט, כחול-בקבוק וקפסולה—מתחילים במרוץ. יחסי ההימורים הם `4` ל-`1`, בלוט; `3` ל-`1`, כחול-בקבוק; `2` ל-`1`, קפסולה. עכשיו, כמה עלי להשקיע על כל סוס כדי לזכות ב-£`13`, לא משנה איזה סוס יגיע ראשון? נניח, לדוגמה, שהימרתי £`5` על כל סוס. אז, אם בלוט ינצח, אקבל £`20` (ארבע פעמים £`5`), ואצטרך לשלם £`5` עבור כל אחד משני הסוסים האחרים; ובכך אזכה ב-£`10`. אבל יתברר שאם כחול-בקבוק יהיה ראשון אזכה רק ב-£`5`, ואם קפסולה תנצח לא ארוויח דבר ולא אפסיד דבר. זה יבהיר את השאלה לחלוטין למתחילים, שכמוני, לא מתעניינים בקריאה של האחווה שמצהירה שהיא עוסקת במשימה הנאצלת של "שיפור גזע הסוסים".

  נושאים:

  אלגברה -> משוואות אלגברה -> בעיות מילוליות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 390

• מרוץ המכוניות

  לפעמים הצהרה פשוטה למדי, אם מנוסחת באופן לא מוכר, תגרום למבוכה ניכרת. הנה דוגמה, וללא ספק היא תבלבל קצת את חלק מקוראי הצעירים יותר שלי. במקרה הייתי במרוץ מכוניות בברוקלנדס, כשצופה אחד אמר למשנהו, בזמן שמספר מכוניות הסתובבו סביב המסלול המעגלי:—

  "הנה גוגלסמית'—האיש הזה במכונית הלבנה!"

  "כן, אני רואה," הייתה התשובה; "אבל כמה מכוניות רצות במרוץ הזה?"

  אז באה התשובה המוזרה הזו:—

  "שליש מהמכוניות שלפני גוגלסמית' ועוד שלושה רבעים מאלה שמאחוריו יתנו לך את התשובה."

  עכשיו, האם אתה יכול לומר כמה מכוניות רצו במרוץ?

  נושאים:

  אלגברה -> משוואות אלגברה -> בעיות מילוליות אריתמטיקה -> שברים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 391

• שאלה

  מצא את כל הפתרונות השלמים `(k>1) y^k=x^2+x`

  נושאים:

  תורת המספרים -> מספרים ראשוניים -> פרוק לגורמים ראשוניים תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • תחרות הערים, תשמ"א, אביב, גרסה עיקרית, כיתות ט-י שאלה 1 נקודות 3

• שאלה

  מצאו מספר דו-ספרתי שהוא פי שתיים גדול יותר ממכפלת ספרותיו.

  נושאים:

  תורת המספרים אריתמטיקה אלגברה -> טכניקה אלגברית קומבינטוריקה -> בדיקת מקרים -> תהליכים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • אתר האינטרנט problems.ru

• שאלה

  בחדר יש כיסאות עם `4` רגליים ועם `3` רגליים. כאשר על כל הכיסאות התיישבו אנשים, נהיה `39` רגליים בחדר (לא נשארו אנשים שעומדים). כמה כיסאות מכל סוג יש בחדר?

  נושאים:

  אלגברה -> בעיות מילוליות תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית -> אלגוריתם אוקלידס אלגברה -> משוואות -> משוואות דיופנטיות

• שאלה

  כמה פתרונות במספרים טבעיים יש למשוואה `(2013 - x)(2013-y)=2013^2` ?

  נושאים:

  תורת המספרים -> מספרים ראשוניים -> פרוק לגורמים ראשוניים אלגברה -> משוואות -> משוואות דיופנטיות
  מקורות:
  • אולימפיאדת בנו ארבל, 2013, כיתה ז שאלה 6

• שאלה

  חרגול יודע לקפוץ `80` סנטימטרים קדימה או `50` סנטימטרים אחורה. האם יכול החרגול להתרחק מהנקודה ההתחלתית תוך פחות מ-`7` קפיצות  למרחק של מטר אחד ו-`70` ס"מ בדיוק?

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  אריתמטיקה תורת המספרים -> משפט השאריות הסיני אלגברה -> בעיות מילוליות הוכחה ודוגמה -> בניית דוגמה קומבינטוריקה -> בדיקת מקרים -> תהליכים אלגברה -> משוואות -> משוואות דיופנטיות

• שאלה

  בארץ הקסומה יש רק שני סוגים של מטבעות: `16` ל"ק (לירות קסומות) ו-`27` ל"ק. האם ניתן לקנות מחברת שעולה לירה קסומה אחת ולקבל עודף מדויק?

  נושאים:

  הוכחה ודוגמה -> בניית דוגמה תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית -> אלגוריתם אוקלידס תורת המספרים -> חלוקה אלגברה -> משוואות -> משוואות דיופנטיות