תורת המספרים

תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.

מספרים ראשוניים משפט השאריות הסיני חשבון השאריות המחלק המשותף המקסימלי והכפולה המשותפת המינימלית מספרים משולשיים חלוקה

  • החידה של פיירו

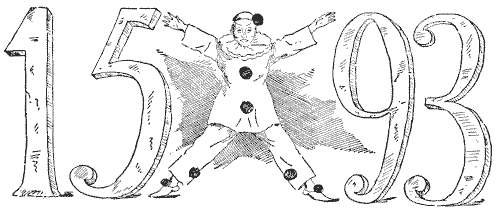    פיירו באיור עומד בתנוחה המייצגת את סימן הכפל. הוא מצביע על העובדה המוזרה ש-`15` כפול `93` מניב בדיוק את אותן הספרות (`1,395`), אך מסודרות באופן שונה. החידה היא לקחת ארבע ספרות כלשהן שתרצו (כולן שונות) ולסדר אותן באופן דומה, כך שהמספר שנוצר מצד אחד של פיירו כאשר הוא מוכפל במספר בצד השני יפיק את אותן הספרות. ישנן דרכים מעטות מאוד לעשות זאת, ואני אתן את כל המקרים האפשריים. האם תוכלו למצוא את כולם? מותר לכם לשים שתי ספרות בכל צד של פיירו כמו בדוגמה המוצגת, או למקם ספרה בודדת בצד אחד ושלוש ספרות בצד השני. אם היינו משתמשים רק בשלוש ספרות במקום בארבע, הדרכים האפשריות היחידות הן אלה: `3` כפול `51` שווה ל-`153`, ו-`6` כפול `21` שווה ל-`126`. מקורות:

  • חידת תגי המספרים

    במקום בו מועסקים מספר רב של פועלים בבניין, נהוג לספק לכל אדם דיסקית קטנה הנושאת את מספרו. דיסקיות אלו נתלות על לוח על ידי הפועלים כשהם מגיעים, ומשמשות כמעקב אחר דייקנות. פעם שמתי לב שמנהל עבודה הסיר מספר תגים אלה מהלוח שלו והניח אותם על טבעת מפוצלת שנשא בכיסו. זה מיד נתן לי את הרעיון לחידה טובה. למעשה, אני אספר לקוראים שלי שכך בדיוק עולים רעיונות לחידות. אתה לא יכול באמת ליצור רעיון: זה קורה - ואתה צריך להיות בכוננות כדי לתפוס אותו כשזה קורה.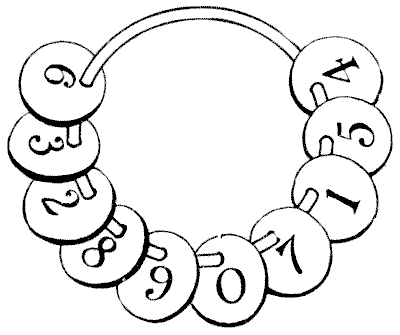 ניתן לראות מהאיור שיש עשרה תגים אלה על טבעת, ממוספרים מ-`1` עד `9` ו-`0`. החידה היא לחלק אותם לשלוש קבוצות מבלי להסיר אף אחד מהם מהטבעת, כך שהקבוצה הראשונה כפול השנייה תיתן את הקבוצה השלישית. לדוגמה, אנו יכולים לחלק אותם לשלוש קבוצות, `2`—`8` `9` `7`—`1` `5` `4` `6` `3`, על ידי הבאת ה-`6` וה-`3` סביב ל-`4`, אבל לצערי שתי הראשונות כשהן מוכפלות יחד לא יוצרות את השלישית. האם אתה יכול להפריד אותם נכון? כמובן שמותר לך שיהיו לך כמה תגים שתרצה בכל קבוצה. החידה דורשת קצת תושייה, אלא אם כן יש לך מזל לפגוע בתשובה במקרה. מקורות:

  • עוד שברים מעורבים

    כשפרסמתי לראשונה את הפתרון שלי לחידה האחרונה, זה הוביל אותי לנסות לבטא את כל המספרים בזה אחר זה עד `100` על ידי שבר מעורב המכיל את כל תשע הספרות. הנה שנים עשר מספרים שהקורא ינסה את כוחו בהם: `13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94`. השתמשו בכל אחת מתשע הספרות פעם אחת בלבד, בכל מקרה.

    מקורות:

  • מספרי ריבוע דיגיטליים

    אלה הן תשע הספרות המסודרות כך שהן יוצרות ארבעה מספרי ריבוע: `9, 81, 324, 576`. עכשיו, האם תוכלו לחבר את כולן יחד כדי ליצור מספר ריבוע יחיד - (I) הקטן ביותר האפשרי, ו- (II) הגדול ביותר האפשרי? מקורות:

  • המספר הקרוע

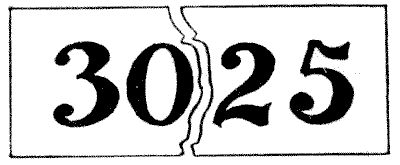
    היתה לי לאחרונה תווית ועליה המספר `3\ 0\ 2\ 5` בספרות גדולות. התווית הזו נקרעה בטעות לשניים, כך ש-`30` היה על חתיכה אחת ו-`25` על השנייה, כפי שמוצג באיור. כשבדקתי את החתיכות האלה התחלתי לעשות חישוב, כמעט בלי לשים לב מה אני עושה, ואז גיליתי את המוזרות הקטנה הזו. אם נחבר את ה-`30` ואת ה-`25` ונעלה את הסכום בריבוע, נקבל כתוצאה את המספר המקורי השלם שהיה על התווית! כלומר, `30` ועוד `25` זה `55`, ו-`55` כפול `55` זה `3025`. מוזר, לא? עכשיו, החידה היא למצוא מספר אחר, המורכב מארבע ספרות, שכולן שונות, שאותו ניתן לחלק באמצע ולקבל את אותה תוצאה.

    מקורות:

  • מספרים מוזרים

    למספר `48` יש תכונה מוזרה זו: אם מוסיפים לו `1`, התוצאה היא מספר ריבועי (`49`, הריבוע של `7`), ואם מוסיפים `1` למחצית שלו, מקבלים גם מספר ריבועי (`25`, הריבוע של `5`). כעת, אין גבול למספרים בעלי תכונה מוזרה זו, וזהו פאזל מעניין למצוא עוד שלושה מהם - המספרים הקטנים ביותר האפשריים. מה הם? מקורות:

  • טעות של מדפיס

    במאמר מסוים, מדפיס היה צריך לסדר את הספרות `5^4xx2^3`, אשר כמובן, משמעותו שהחזקה הרביעית של `5` (`625`) צריכה להיות מוכפלת בחזקה השלישית של `2` (`8`), שהמכפלה שלהם היא `5,000`. אבל הוא הדפיס את `5^4xx2^3` כ- `5\ 4\ 2\ 3`, וזה לא נכון. האם תוכלו למקם ארבע ספרות באופן המוצג, כך שזה יהיה נכון באותה מידה אם המדפיס יסדר אותן כראוי או יעשה את אותה טעות?

    מקורות:

  • הקפת הריבועים

     

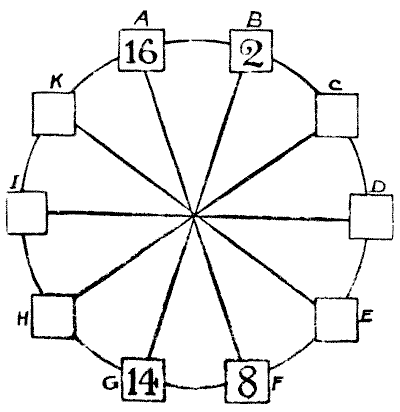
    החידה היא להציב מספר שונה בכל אחד מעשרת הריבועים כך שסכום ריבועי כל שני מספרים סמוכים יהיה שווה לסכום ריבועי שני המספרים הנמצאים בדיוק מולם במעגל. ארבעת המספרים המוצבים כדוגמאות חייבים להישאר במקומם. ריבוע של `16` הוא `256`, וריבוע של `2` הוא `4`. חברו אותם יחד, והתוצאה היא `260`. כמו כן—ריבוע של `14` הוא `196`, וריבוע של `8` הוא `64`. גם אלה יחד יוצרים `260`. עכשיו, באותו אופן בדיוק, B ו-C צריכים להיות שווים ל-G ו-H (הסכום לא בהכרח יהיה `260`), A ו-K ל-F ו-E, H ו-I ל-C ו-D, וכן הלאה, עם כל שני ריבועים סמוכים במעגל.

    כל שעליכם לעשות הוא למלא את ששת המספרים הנותרים. שברים אינם מותרים, ואני אראה שאף מספר לא צריך להכיל יותר משתי ספרות.

    מקורות:

  • בעיה בריבועים

    יש ברשותנו שלושה לוחות מרובעים. שטח הפנים של הראשון מכיל חמישה רגל רבוע יותר מהשני, והשני מכיל חמישה רגל רבוע יותר מהשלישי. האם תוכלו לתת מידות מדויקות עבור צלעות הלוחות? אם תוכלו לפתור את החידה הקטנה הזו, נסו למצוא שלושה ריבועים בסדרה חשבונית, עם הפרש קבוע של `7` וגם של `13`. מקורות:

  • קרב הייסטינגס

    כל ההיסטוריונים יודעים שיש מידה רבה של מסתורין וחוסר ודאות בנוגע לפרטי הקרב הבלתי נשכח לעולם באותו יום גורלי, `14` באוקטובר `1066`. החידה שלי עוסקת בקטע מוזר בכרוניקה נזירית עתיקה שאולי לעולם לא תקבל את תשומת הלב הראויה לה, ואם אינני יכול לערוב לאותנטיות של המסמך, הוא בכל זאת ישמש אותנו כדי לספק לנו בעיה שקשה שלא תעניין את אותם קוראים שלי שיש להם נטיות אריתמטיות. הנה הקטע המדובר.

    "אנשיו של הרולד עמדו יחד היטב, כמנהגם, ויצרו שישים ואחת ריבועים, עם מספר שווה של אנשים בכל ריבוע מהם, ואוי לנורמני האמיץ שהעז להיכנס למעוזיהם; שכן מכה בודדת של גרזן מלחמה סקסוני תשבור את חניתו ותחתוך את מעיל השרשראות שלו.... כאשר הרולד השליך את עצמו לתוך המהומה, הסקסונים היו ריבוע אדיר אחד של אנשים, שצועקים את קריאות הקרב, 'Ut!' 'Olicrosse!' 'Godemitè!'"

    כעת, אני מגלה שכל הרשויות העכשוויות מסכימות שהסקסונים אכן נלחמו בסדר מוצק זה. לדוגמה, ב"Carmen de Bello Hastingensi," שיר המיוחס לגאי, הבישוף של אמיין, שחי בתקופת הקרב, נאמר לנו ש"הסקסונים עמדו קבועים במסה צפופה," והנרי מהנטינגדון רושם ש"הם היו כמו טירה, בלתי חדירים לנורמנים;" בעוד רוברט וייס, כעבור מאה שנה, מספר לנו את אותו הדבר. אז מבחינה זו הכרוניקה החדשה שלי עשויה שלא לטעות כל כך. אבל יש לי סיבה להאמין שמשהו לא בסדר עם המספרים בפועל. תן לקורא לראות מה הוא יכול לעשות מהם.

    מספר האנשים יהיה שישים ואחת פעמים מספר ריבועי; אבל כאשר הרולד עצמו הצטרף למהומה, הם הצליחו ליצור ריבוע גדול אחד. מהו המספר הקטן ביותר האפשרי של אנשים שיכולים היו להיות שם?

    כדי להבהיר לקורא את הפשטות של השאלה, אתן את הפתרונות הנמוכים ביותר במקרה של `60` ו-`62`, המספרים שמיד לפני ואחרי `61`. הם `60xx4^2+1 = 31^2`, ו-`62xx8^2+1=63^2`. כלומר, `60` ריבועים של `16` אנשים כל אחד יהיו `960` אנשים, וכאשר הרולד הצטרף אליהם הם יהיו `961` במספר, וכך יצרו ריבוע עם `31` אנשים בכל צד. באופן דומה במקרה של המספרים שנתתי עבור `62`. עכשיו, מצא את התשובה הנמוכה ביותר עבור `61`.

    מקורות: