תורת המספרים
תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.
מספרים ראשוניים משפט השאריות הסיני חשבון השאריות המחלק המשותף המקסימלי והכפולה המשותפת המינימלית מספרים משולשיים חלוקה-
ביטוי שלם
מצאו את כל ה n השלמים עבורם הביטוי `{(n+2)^4}/{n-1}` מוגדר ושלם.
מקורות: -
הספְרָה ה-1224
כותבים את המספרים הטבעיים על פי סדר, זה אחר זה משמאל לימין:
1234567891011...
נשים לב למשל, שהספרה במקום ה-10 היא 1 ושהספרה במקום ה-11 היא 0.
ממשיכים עם הכתיבה הזו, כמה שצריך...
איזו ספרה תהיה במקום ה-1224 ברצף?
מקורות: -
פולינום עם מקדמים שלמים
יהי (p(x פולינום עם מקדמים שלמים המקיים `p(-2006) < p(2006)=2005`. הוכח ש- `p(-2006)<=-2007`.
מקורות:
- תחרות גרוסמן, 2006 שאלה 6
-
שאלה
תלמידי כיתה ח' זרקו כדורי גומי לקופסה ואחר כך ניסו לנחש כמה כדורים הצטברו שם. חמישה תלמידים ניסו לנחש: 45, 41, 55, 50, 43, אך אף אחד לא ניחש בדיוק את הכמות. הניחושים נבדלו מהאמת ב- 3, 7, 5, 7 ו-2 כדורים (לא בהכרח באותו הסדר כמו הניחושים). כמה כדורים היו בקופסה?
מקורות:נושאים:תורת המספרים אריתמטיקה אלגברה -> בעיות מילוליות לוגיקה -> הגיון קומבינטוריקה -> בדיקת מקרים -> תהליכים -
שאלה
בתרגיל אותיות זהות מסמנות ספרות זהות, אותיות שונות ספרות שונות, כוכביות מסמנות ספרות כלשהן. מצאו את כל הספרות.
`(ABCD)^2 = A B ** ** ** C D `מקורות:נושאים:תורת המספרים אריתמטיקה קומבינטוריקה -> בדיקת מקרים -> תהליכים חידות ורבוסים -> שחזרו את התרגיל -
שאלה
מצאו את המספר `c` הקטן ביותר, כך שלמשוואה `3x + 4y = c` יהיו בדיוק 3 פתרונות במספרים שלמים חיוביים.
מקורות: -
שאלה
החליפו אותיות בספרות שונות מאפס, כך שתתקבל זהות נכונה. אותיות זהות מסמנות ספרות זהות, אותיות שונות – ספרות שונות; גל, גר הם מספרים דו-ספרתיים שמורכבים מספרות אלו.
מקורות:
`ל / ג + ל/ר + ל/ב + ל/(רג) + ל/ (ל ג) = ל` -
חידת הלוקרים
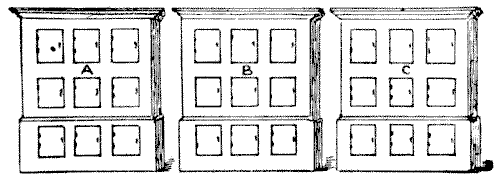
לאיש היו במשרדו שלושה ארונות, שבכל אחד מהם תשעה לוקרים, כפי שמוצג בדיאגרמה. הוא הורה לפקיד שלו להציב ספרה שונה על כל לוקר בארון A, ולעשות את אותו הדבר בארון B ובארון C. מכיוון שמותר לנו כאן לקרוא לאפס ספרה, ולא נאסר עליו להשתמש באפס כמספר, ברור שהייתה לו האפשרות להשמיט כל אחת מעשר הספרות מכל ארון.
כעת, המעסיק לא אמר שהלוקרים ימוספרו בסדר מספרי כלשהו, והוא הופתע לגלות, לאחר שהעבודה הסתיימה, שהספרות כנראה עורבבו באופן אקראי. כשקרא לפקיד שלו להסבר, הנער האקסצנטרי הצהיר שהעלתה בדעתו המחשבה לסדר את הספרות כך שבכל מקרה הן יצרו תרגיל חיבור פשוט, כאשר שתי השורות העליונות של הספרות יוצרות את הסכום בשורה התחתונה. אבל הנקודה המפתיעה ביותר הייתה זו: שהוא סידר אותן כך שהחיבור ב-A נתן את הסכום הקטן ביותר האפשרי, שהחיבור ב-C נתן את הסכום הגדול ביותר האפשרי, וכי כל תשע הספרות בסך הכל בשלושת הסכומים היו שונות. החידה היא להראות כיצד ניתן לעשות זאת. אין לאפשר עשרונים והאפס אינו יכול להופיע במקום המאות.
מקורות: -
שלוש הקבוצות
בכתב העת "Nouvelles Annales de Mathématiques" הופיעה החידה הבאה כשינוי לאחת מ"חידות קנטרברי" שלי. סדר את תשע הספרות בשלוש קבוצות של שתיים, שלוש וארבע ספרות, כך ששני המספרים הראשונים כאשר מכפילים אותם זה בזה יוצרים את השלישי. לדוגמה, `12` × `483` = `5,796`. אני מציע כעת לכלול גם את המקרים שבהם יש ספרה אחת, ארבע וארבע ספרות, כגון `4` × `1,738` = `6,952`. האם תוכל למצוא את כל הפתרונות האפשריים בשני המקרים? מקורות: -
כפל ספרותי
הנה בעיה משעשעת נוספת עם תשע הספרות, כאשר הספרה אפס אינה נכללת. באמצעות כל ספרה פעם אחת בלבד, אנו יכולים ליצור שני תרגילי כפל בעלי מכפלה זהה, וניתן לעשות זאת בדרכים רבות. לדוגמה, 7x658 ו-14x329 מכילים את כל הספרות פעם אחת, והמכפלה בכל מקרה זהה - `4,606`. כעת, ניתן לראות שסכום הספרות במכפלה הוא `16`, שאינו הסכום הגבוה או הנמוך ביותר שניתן להשיג. האם תוכלו למצוא את הפתרון לבעיה שנותן את הסכום הנמוך ביותר האפשרי של ספרות במכפלה המשותפת? וגם את זה שנותן את הסכום הגבוה ביותר האפשרי? מקורות: