תורת המספרים
תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.
מספרים ראשוניים משפט השאריות הסיני חשבון השאריות המחלק המשותף המקסימלי והכפולה המשותפת המינימלית מספרים משולשיים חלוקה-
החידה של הבנקאי
לבנקאי היה לקוח הרפתקן שתמיד היה להוט להמר על כל דבר. בתקווה לרפא אותו מההרגל הרע שלו, הוא הציע כהימור שהלקוח לא יוכל לחלק את תכולת קופסה המכילה רק שישה פני לחלוקה למספר מדויק של ערימות שוות של שישה פני. הבנקאי היה הראשון להכניס שישה פני אחד או יותר (כמה שרצה); ואז הלקוח היה אמור להכניס שישה פני אחד או יותר (אך במקרה שלו לא יותר מלירה אחת בערך), כאשר אף אחד מהם לא יודע מה השני הכניס. לבסוף, הלקוח היה אמור להעביר מדלפק הבנקאי לקופסה כמה שישה פני שהבנקאי ביקש ממנו להכניס. החידה היא למצוא כמה שישה פני הבנקאי צריך להכניס תחילה וכמה הוא צריך לבקש מהלקוח להעביר, כדי שיהיה לו הסיכוי הטוב ביותר לנצח. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 134
-
נשות ההולנדים
אני תוהה כמה מהקוראים שלי מכירים את החידה של "נשות ההולנדים" —שבה עליכם לקבוע את שמות נשותיהם של שלושה גברים, או, ליתר דיוק, איזו אישה שייכת לכל בעל. לפני כשלושים שנה זה "עבר בין כולם," כמשהו די חדש, אך לאחרונה גיליתי זאת ב-Ladies' Diary עבור `1739-40`, כך שזה היה מוכר בבירור למין היפה לפני יותר ממאה ושבעים שנה. כמה מאמותינו, נשותינו, אחיותינו, בנותינו ודודותינו יוכלו לפתור את החידה היום? נקווה שאחוז גדול בהרבה מאשר אז.
שלושה הולנדים, בשמות הנדריק, אלס וקורנליוס, ונשותיהם, גורטרון, קטרון ואנה, קונים חזירים. כל אחד קונה כמספר השילינגים שהוא (או היא) נותן עבור אחד. כל בעל משלם בסך הכל שלושה גינאה יותר מאשתו. הנדריק קונה עשרים ושלושה חזירים יותר מקטרון, ואלס אחד-עשר יותר מגורטרון. עכשיו, מה היה שמה של אשת כל גבר?
 מקורות:נושאים:תורת המספרים -> מספרים ראשוניים אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> משוואות -> משוואות דיופנטיות
מקורות:נושאים:תורת המספרים -> מספרים ראשוניים אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> משוואות -> משוואות דיופנטיות- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 139
-
ריבועי קסם מדרגה שנייה
בזמן שקראתי חיבור מתמטי צרפתי, נתקלתי בהצהרה הבאה: "ריבוע קסם מדהים ביותר מסדר `8`, בשתי דרגות, נבנה על ידי מר פפרמן. במילים אחרות, הוא הצליח לסדר את שישים וארבעת המספרים הראשונים על משבצות לוח השחמט בצורה כזו שסכום המספרים בכל שורה, בכל טור ובכל אחד משני האלכסונים יהיה זהה; ויותר מכך, אם נחליף את כל המספרים בריבועים שלהם, הריבוע עדיין יישאר קסום." מיד ניגשתי לעבודה כדי לפתור את הבעיה הזו, ולמרות שהיא התבררה כאגוז קשה לפיצוח, זכיתי בגילוי של כמה חוקים מוזרים ויפים השולטים בה. ייתכן שהקורא ירצה לנסות את כוחו בפאזל.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 408
-
סלי הפירות
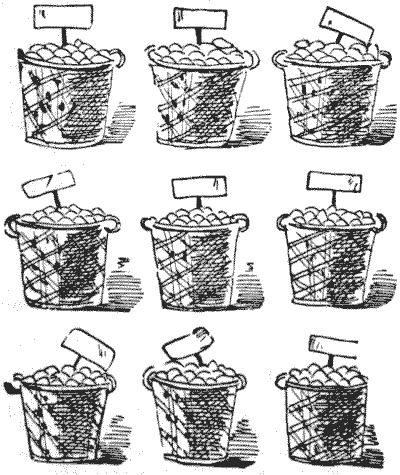
זו הצורה שבה הצגתי לראשונה את השאלה של ריבועים קסומים עם מספרים ראשוניים. אני כאן מזהיר את הקורא שיש מלכודת קטנה.
לסוחר פירות היו תשעה סלים. כל סל הכיל שזיפים (כולם שלמים ובשלים), והמספר בכל סל היה שונה. כאשר הם הוצבו כפי שמוצג באיור, הם יצרו ריבוע קסם, כך שאם הוא היה לוקח כל שלושה סלים בקו בשמונה הכיוונים האפשריים, תמיד יהיה אותו מספר של שזיפים. החלק הזה של הפאזל קל מספיק להבנה. אבל מה שבא לאחר מכן נראה ממבט ראשון קצת מוזר.
הסוחר אמר לאחד מעובדיו לחלק את תכולת הסל שהוא יבחר בין כמה ילדים, ולתת שזיפים לכל ילד כך שכל אחד יקבל מספר שווה. אבל העובד גילה שזה בלתי אפשרי לחלוטין, לא משנה איזה סל הוא בחר ולא משנה כמה ילדים הוא כלל בפינוק. הראה, על ידי מתן תכולת תשעת הסלים, כיצד זה יכול לקרות.
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 409
-
החידה בצורת "T" של המנדרין
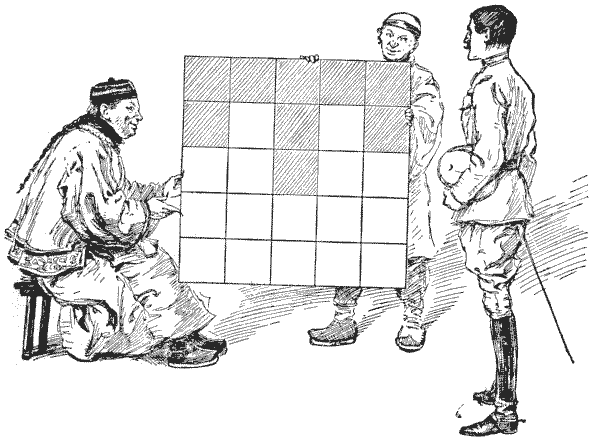
לפני שמארג׳וריבנקס בושאמפ צ׳ולמונדלי יצא לסיורו במזרח הרחוק, הוא התגאה בידע שלו בריבועים קסומים, נושא שהפך לתחביב מיוחד שלו; אבל עד מהרה הוא גילה שמעולם לא נגע יותר מאשר בשולי הנושא, ושצ׳יני ערמומי יכול לנצח אותו בקלות. אני מציג בעיה קטנה שמנדרין מלומד הציג למטייל שלנו, כפי שמצויר בעמוד האחרון.
הסיני, לאחר שהעיר שהבנייה של ריבוע קסם רגיל של עשרים וחמישה תאים היא "too velly muchee easy," ביקש מבן ארצנו למקם את המספרים `1` עד `25` בריבוע כך שכל עמודה, כל שורה וכל אחד משני האלכסונים יסתכמו ל-`65`, כאשר רק מספרים ראשוניים נמצאים על ה-"T" המוצלל. כמובן שהמספרים הראשוניים הזמינים הם `1, 2, 3, 5, 7, 11, 13, 17, 19`, ו-`23`, כך שיש לך חופש לבחור כל תשעה מהם שישרתו את מטרתך. האם אתה יכול לבנות את ריבוע הקסם הקטן והסקרן הזה?
מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 410
-
ריבוע קסם של מספרים מורכבים
כפי שדנו זה עתה בבניית ריבועי קסם עם מספרים ראשוניים, הבעיה הבאה מהווה בעיה נלווית מעניינת. בנו ריבוע קסם עם תשעה מספרים מורכבים עוקבים - הקטן ביותר האפשרי.מקורות:נושאים:תורת המספרים -> מספרים ראשוניים- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 411
-
שאלה
חרגול יודע לקפוץ `80` סנטימטרים קדימה או `50` סנטימטרים אחורה. האם יכול החרגול להתרחק מהנקודה ההתחלתית תוך פחות מ-`7` קפיצות למרחק של מטר אחד ו-`70` ס"מ בדיוק?
נושאים:אריתמטיקה תורת המספרים -> משפט השאריות הסיני אלגברה -> בעיות מילוליות הוכחה ודוגמה -> בניית דוגמה קומבינטוריקה -> בדיקת מקרים -> תהליכים אלגברה -> משוואות -> משוואות דיופנטיות -
שאלה
הוכיחו כי קיימות שתי חזקות של `2` שהפרש שלהן מתחלק ב-`2017`.
מקורות: -
שאלה
בהינתן מספר שלם חיובי N, נתבונן בתהליך הבא: נסמן ב-`S(N)` את סכום הספרות של N ניקח את סכום הספרות של `S(N)` נחזור על הפעולה שוב ושוב עד שנקבל מספר חד ספרתי נקרא למספר הפעמים שביצענו את התהליך הנ"ל עד שקיבלנו מספר חד-ספרתי: "העומק" של N. לדוגמה, העומק של 49 הוא `S(49)=13 -> S(13)=4)2` , הפעולה בוצעה פעמיים( והעומק של 45 הוא 1.
א) הוכיחו כי לכל מספר N אכן יש עומק סופי, כלומר, שתמיד יתקבל מספר חד-ספרתי בשלב כלשהו של התהליך.
ב) נסמן ב-`x(n)` את המספר המינימלי (שערכו הקטן ביותר) בעל עומק N. מצאו את השארית של `x(5776)` בחילוק ב-6 .נמקו את תשובתכם!
ג) מצאו את השארית של המספר `x(5776) - x(5708)` בחילוק ב-2016 .נמקו את תשובתכם!
מקורות:- אולימפיאדת גיליס, תשע"ו שאלה 3
-
שאלה
הוכיחו כי מבין חמישה מספרים שלמים ניתן לבחור שניים שהפרש שלהם מתחלק ב-`4`.
נושאים:תורת המספרים -> חשבון השאריות קומבינטוריקה -> עקרון שובך היונים תורת המספרים -> חלוקה -> זוגיות אריתמטיקה -> חילוק עם שארית