תורת המספרים

תורת המספרים היא ענף במתמטיקה העוסק בתכונות של מספרים שלמים. נושאים כוללים מספרים ראשוניים, חלוקה, קונגרואנציות (חשבון מודולרי), משוואות דיופנטיות ופונקציות של מספרים שלמים. שאלות דורשות לעיתים קרובות חשיבה אנליטית ויצירתית על מספרים.

מספרים ראשוניים משפט השאריות הסיני חשבון השאריות המחלק המשותף המקסימלי והכפולה המשותפת המינימלית מספרים משולשיים חלוקה

  • הבעיה של הפסל

    פסל קדום הוזמן לספק שני פסלים, כל אחד על גבי כן מעוקב. אנו עוסקים בכנים אלה. הם היו בגדלים שונים, כפי שניתן לראות באיור, וכאשר הגיע הזמן לתשלום התגלעה מחלוקת בשאלה האם ההסכם התבסס על מדידה קווית או מעוקבת. אך ברגע שהם באו למדוד את שני הכנים, העניין הוסדר מיד, מכיוון שמספר הרגליים הקווי היה זהה בדיוק למספר הרגליים המעוקב. החידה היא למצוא את המידות לשני כנים בעלי תכונה זו, במספרים הקטנים ביותר האפשריים. אתם מבינים, אם שני הכנים, למשל, מודדים `3` רגל ו-`1` רגל בכל צד, אז המדידה הקווית תהיה `4` רגל והתכולה המעוקבת `28` רגל, שאינם זהים, כך שהמידות האלה לא יתאימו. מקורות:

  • הקמצן הספרדי

    בעיירה קטנה בקסטיליה החדשה חי פעם קמצן ידוע בשם דון מנואל רודריגז. אהבתו לכסף הושוותה רק לתשוקה עזה לבעיות אריתמטיות. חידות אלה עסקו בדרך כלל באופן כזה או אחר באוצרותיו שנצברו, והוצעו על ידו אך ורק כדי שיוכל ליהנות מלפתור אותן בעצמו. למרבה הצער, רק מעטות מהן שרדו, וכאשר טיילתי בספרד, ואספתי חומר לעבודה מוצעת על "הבצל הספרדי כגורם לשקיעה לאומית", גיליתי רק מעטות מאוד. אחת מהן עוסקת בשלוש הקופסאות המופיעות בפורטרט האותנטי המצורף. כל קופסה הכילה מספר שונה של דובלוני זהב. ההפרש בין מספר הדובלונים בקופסה העליונה למספר בקופסה האמצעית היה זהה להפרש בין המספר בקופסה האמצעית למספר בקופסה התחתונה. ואם תכולתן של שתיים כלשהן מהקופסאות היו מאוחדות, הן היו יוצרות מספר ריבועי. מהו המספר הקטן ביותר של דובלונים שיכול היה להיות באחת מהקופסאות? מקורות:

  • תשע תיבות האוצר

    החידה הבאה תמחיש את החשיבות של היכולת לקבוע את הגבולות המינימליים והמקסימליים של מספר נדרש. לעתים קרובות ניתן לעשות זאת. לדוגמה, טרם התברר בכמה דרכים שונות ניתן לבצע את מסע הפרש על לוח השחמט; אבל אנו יודעים שזה פחות ממספר הצירופים של `168` דברים שנלקחו `63` בכל פעם ויותר מ-`31,054,144`—כי האחרון הוא מספר המסלולים מסוג מסוים. או, כדי לקחת מקרה מוכר יותר, אם תשאל אדם כמה מטבעות יש לו בכיס, הוא עשוי לומר לך שאין לו מושג קלוש. אבל בחקירה נוספת תוציא ממנו הצהרה כגון: "כן, אני בטוח שיש לי יותר משלושה מטבעות, ובאותה מידה בטוח שאין כל כך הרבה כמו עשרים וחמישה." כעת, הידיעה שמספר מסוים נמצא בין `2` ל-`12` בחידה שלי תאפשר לפותר למצוא את התשובה המדויקת; ללא מידע זה יהיה מספר אינסופי של תשובות, מהן לא ניתן יהיה לבחור את הנכונה.

    זוהי חידה נוספת שהתקבלה מחברי דון מנואל רודריגז, הקמצן התמהוני של ניו קסטיליה. בערב ראש השנה האזרחית בשנת `1879` הוא הראה לי תשע תיבות אוצר, ולאחר שהודיע לי שכל תיבה הכילה מספר ריבועי של דובלונים מוזהבים, ושההפרש בין תכולת A ו-B היה זהה לזה שבין B ו-C, D ו-E, E ו-F, G ו-H, או H ו-I, הוא ביקש ממני לומר לו את מספר המטבעות בכל אחת מהקופסאות. בהתחלה חשבתי שזה בלתי אפשרי, שכן יהיה מספר אינסופי של תשובות שונות, אבל לאחר מחשבה גיליתי שזה לא המקרה. גיליתי שבעוד שכל תיבה הכילה מטבעות, התכולה של A, B, C גדלה במשקל בסדר אלפביתי; כך גם D, E, F; וכך גם G, H, I; אבל D או E לא צריכים להיות כבדים יותר מ-C, וגם G או H לא צריכים להיות כבדים יותר מ-F. כמו כן, היה ברור לחלוטין שתיבה A לא יכולה להכיל יותר מתריסר מטבעות מבחוץ; ייתכן שלא יהיה חצי מהמספר הזה, אבל הייתי בטוח שלא היו יותר משנים עשר. עם הידע הזה הצלחתי להגיע לתשובה הנכונה.

    בקיצור, עלינו לגלות תשעה מספרים ריבועיים כך ש-A, B, C; ו-D, E, F; ו-G, H, I הן שלוש קבוצות בסדרה חשבונית, כאשר ההפרש הקבוע זהה בכל קבוצה, ו-A קטן מ-`12`. כמה דובלונים היו בכל אחת מתשע התיבות?

    מקורות:

  • חמשת השודדים

    חמשת השודדים הספרדים, אלפונסו, בניטו, קרלוס, דייגו ואסטבן, ספרו את שללם לאחר פשיטה, כאשר התגלה שהם שדדו יחד בדיוק `200` דובלונים. אחד מהחבורה ציין שאם לאלפונסו יהיה פי שנים עשר, לבניטו פי שלושה, לקרלוס אותו סכום, לדייגו חצי מהסכום ולאסטבן שליש מהסכום, עדיין יהיו להם יחד בדיוק `200` דובלונים. כמה דובלונים היו לכל אחד?

    ישנן תשובות נכונות רבות באותה מידה לשאלה זו. הנה אחת מהן:

    A 6 × 12 = 72
    B 12 × 3 = 36
    C 17 × 1 = 17
    D 120 × ½ = 60
    E 45 × 1/3 = 15
      200       200

    החידה היא לגלות בדיוק כמה תשובות שונות יש, בהנחה שלכל אחד היה משהו ושאסור שיהיה כסף חלקי — רק דובלונים בכל מקרה.

    בעיה זו, שניסוחה שונה במקצת, הוצגה על ידי טרטליה (נפטר ב-`1559`), והוא החמיא לעצמו שהוא מצא פתרון אחד; אבל מתמטיקאי צרפתי ידוע (M.A. Labosne), בעבודה מהעת האחרונה, אומר שקוראיו יופתעו כאשר הוא מבטיח להם שיש `6,639` תשובות נכונות שונות לשאלה. האם זה כך? כמה תשובות יש?

    מקורות:

  • הבעיה של סתת האבנים

    לסתת אבנים היה פעם מספר גדול של קוביות אבן בחצר שלו, כולן באותו גודל בדיוק. היו לו כמה הרגלים קטנים דמיוניים מאוד, ואחד הרעיונות המוזרים שלו היה לשמור את הבלוקים האלה מוערמים בערימות מעוקבות, כך שאין שתי ערימות שמכילות את אותו מספר בלוקים. הוא גילה בעצמו (עובדה שידועה היטב למתמטיקאים) שאם הוא היה לוקח את כל הבלוקים הכלולים במספר כלשהו של ערימות בסדר רגיל, החל מהקוביה הבודדת, הוא תמיד יכול היה לסדר אותם על הקרקע כדי ליצור ריבוע מושלם. זה יהיה ברור לקורא, מכיוון שבלוק אחד הוא ריבוע, `1+8 = 9` הוא ריבוע, `1+8+27=36` הוא ריבוע, `1+8+27+64=100` הוא ריבוע, וכן הלאה. למעשה, סכום כל מספר של קוביות עוקבות, החל תמיד מ-`1`, הוא בכל מקרה מספר ריבועי.

    יום אחד נכנס ג'נטלמן לחצר של הבנאי והציע לו מחיר מסוים אם יספק לו מספר עוקב של ערימות מעוקבות אלה, שאמורות להכיל יחד מספר בלוקים שניתן לפרוס ליצירת ריבוע, אך הקונה התעקש על יותר משלוש ערימות וסירב לקחת את הבלוק הבודד מכיוון שהיה בו פגם. מה היה המספר הקטן ביותר האפשרי של בלוקי אבן שהבנאי היה צריך לספק?

    מקורות:

  • המתנה לחג המולד של גברת סמיילי

    הבעת ההנאה של גברת סמיילי הייתה כנה כאשר שש נכדותיה שלחו לה, כמתנה לחג המולד, שמיכת טלאים יפה מאוד, שהן הכינו במו ידיהן. היא נבנתה מחתיכות מרובעות של חומר משי, כולן באותו גודל, ומכיוון שהן הכינו שמיכה גדולה עם ארבעה עשר ריבועים קטנים אלה בכל צד, ברור שנתפרו לתוכה בדיוק `196` חתיכות. עכשיו, שש הנכדות תרמו כל אחת חלק מהעבודה בצורה של ריבוע מושלם (כל ששת החלקים בגודל שונה), אך כדי לחבר אותם ליצירת השמיכה המרובעת היה צורך לפרום את עבודתה של ילדה אחת לשלושה חלקים נפרדים. האם תוכלו להראות כיצד ניתן היה לבצע את החיבורים? כמובן, שאף חלק לא ניתן להפוך.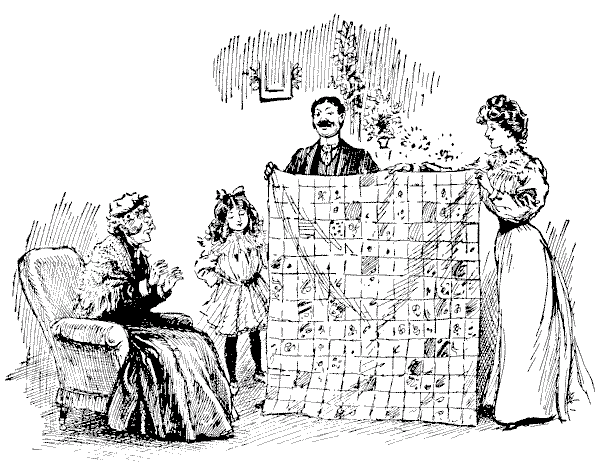 מקורות:

  • טריק עם קוביות

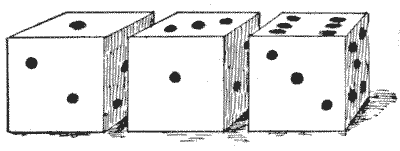    הנה טריק קטן ונחמד עם שלוש קוביות. אני מבקש ממך לזרוק את הקוביות מבלי שאראה אותן. לאחר מכן אני אומר לך להכפיל את הנקודות של הקוביה הראשונה ב-`2` ולהוסיף `5`; ואז להכפיל את התוצאה ב-`5` ולהוסיף את הנקודות של הקוביה השנייה; ואז להכפיל את התוצאה ב-`10` ולהוסיף את הנקודות של הקוביה השלישית. לאחר מכן אתה נותן לי את הסכום הכולל, ואני יכול מיד לומר לך את הנקודות שנזרקו בשלוש הקוביות. איך אני עושה את זה? לדוגמה, אם זרקת `1, 3`, ו-`6`, כפי שמוצג באיור, התוצאה שהיית נותן לי תהיה `386`, שממנה אוכל מיד לומר מה זרקת. מקורות:

  • רצועות הקסם

     

    קרה שהיו מונחות על השולחן שלי מספר רצועות קרטון, ועליהן מודפסים מספרים מ-`1` ומעלה בסדר עולה. עלה בי הרעיון לפתע, כפי שלרעיונות יש נטייה להופיע באופן בלתי צפוי, ליצור חידה קטנה. אני תוהה אם קוראים רבים יגיעו לאותו פתרון שאני הגעתי אליו.

    קחו שבע רצועות קרטון והניחו אותן יחד כפי שמוצג לעיל. לאחר מכן כתבו על כל אחת מהן את המספרים `1, 2, 3, 4, 5, 6, 7`, כפי שמוצג, כך שהמספרים ייצרו שבע שורות ושבע עמודות.

    כעת, החידה היא לחתוך את הרצועות הללו למספר המועט ביותר של חלקים, כך שניתן יהיה להניח אותם יחד וליצור ריבוע קסם, כאשר שבע השורות, שבע העמודות ושני האלכסונים מסתכמים לאותו מספר. אסור להפוך או להניח אף ספרה על צידה — כלומר, כל הרצועות חייבות להיות מונחות בכיוון המקורי שלהן.

    כמובן שאפשר לחתוך כל רצועה לשבעה חלקים נפרדים, כאשר כל חלק מכיל מספר, והחידה תהיה קלה מאוד, אבל אני לא צריך לומר שארבעים ותשעה חלקים רחוקים מאוד מלהיות המספר המועט ביותר האפשרי.

    מקורות:

  • הצינוקים הסיביריים

     

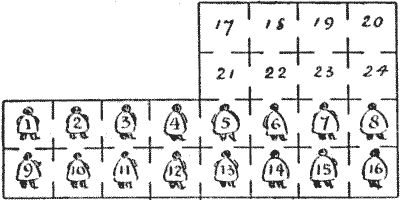
    למעלה מוצגת תוכנית מהימנה של בית כלא רוסי מסוים בסיביר. כל התאים ממוספרים, והאסירים ממוספרים במספרים זהים לתאים בהם הם נמצאים. תזונת הכלא כל כך משמינה שאסירים פוליטיים אלה חוששים תמידית שאם יגיע חנינה, הם לא יוכלו לדחוס את עצמם דרך הפתחים הצרים ולצאת. וכמובן שזה יהיה לא סביר לבקש מכל ממשלה להפיל את חומות הכלא רק כדי לשחרר את האסירים, יהיו אשר יהיו חפים מפשע. לכן אנשים אלה עושים את כל הפעילות הגופנית הבריאה שהם יכולים כדי לעכב את ההשמנה הגוברת שלהם, ואחד הבילויים שלהם ישמש אותנו כדי לספק את החידה הבאה.

    הראו, במספר המהלכים המועט ביותר האפשרי, כיצד ששת-עשר האסירים יכולים לסדר את עצמם בריבוע קסם, כך שהמספרים על גבם יסתכמו לאותו סכום בכל אחד מארבעת הטורים, ארבע השורות ושני האלכסונים, מבלי ששני אסירים היו אי פעם באותו תא יחד. מוטב שאומר, לידיעת אלה שעדיין לא הכירו את המקומות האלה, שאחת המוזרויות של בתי הכלא היא שלא מורשים לצאת מגבולות החומות שלהם. כל אסיר רשאי ללכת כל מרחק אפשרי במהלך בודד.

    מקורות:

  • שאלה

    נתון מספר ראשוני תלת-ספרתי שכל ספרותיו שונות. ידוע שהספרה האחרונה שלו שווה לסכום של שתי הספרות האחרות. מצאו את כל האפשרויות לספרה האחרונה של המספר הזה.

    מקורות: