אלגברה

אלגברה היא ענף רחב במתמטיקה המשתמש בסמלים (בדרך כלל אותיות) לייצוג מספרים ולהצגת כללים ויחסים. היא כוללת מניפולציה של ביטויים, פתרון משוואות ואי-שוויונים, וחקר פונקציות ומבנים. שאלות מכסות מגוון רחב של נושאים אלו.

טכניקה אלגברית משוואות אי שוויונים בעיות מילוליות סדרות

  • המספר הקרוע

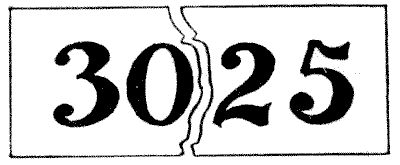
    היתה לי לאחרונה תווית ועליה המספר `3\ 0\ 2\ 5` בספרות גדולות. התווית הזו נקרעה בטעות לשניים, כך ש-`30` היה על חתיכה אחת ו-`25` על השנייה, כפי שמוצג באיור. כשבדקתי את החתיכות האלה התחלתי לעשות חישוב, כמעט בלי לשים לב מה אני עושה, ואז גיליתי את המוזרות הקטנה הזו. אם נחבר את ה-`30` ואת ה-`25` ונעלה את הסכום בריבוע, נקבל כתוצאה את המספר המקורי השלם שהיה על התווית! כלומר, `30` ועוד `25` זה `55`, ו-`55` כפול `55` זה `3025`. מוזר, לא? עכשיו, החידה היא למצוא מספר אחר, המורכב מארבע ספרות, שכולן שונות, שאותו ניתן לחלק באמצע ולקבל את אותה תוצאה.

    מקורות:

  • מספרים מוזרים

    למספר `48` יש תכונה מוזרה זו: אם מוסיפים לו `1`, התוצאה היא מספר ריבועי (`49`, הריבוע של `7`), ואם מוסיפים `1` למחצית שלו, מקבלים גם מספר ריבועי (`25`, הריבוע של `5`). כעת, אין גבול למספרים בעלי תכונה מוזרה זו, וזהו פאזל מעניין למצוא עוד שלושה מהם - המספרים הקטנים ביותר האפשריים. מה הם? מקורות:

  • טעות של מדפיס

    במאמר מסוים, מדפיס היה צריך לסדר את הספרות `5^4xx2^3`, אשר כמובן, משמעותו שהחזקה הרביעית של `5` (`625`) צריכה להיות מוכפלת בחזקה השלישית של `2` (`8`), שהמכפלה שלהם היא `5,000`. אבל הוא הדפיס את `5^4xx2^3` כ- `5\ 4\ 2\ 3`, וזה לא נכון. האם תוכלו למקם ארבע ספרות באופן המוצג, כך שזה יהיה נכון באותה מידה אם המדפיס יסדר אותן כראוי או יעשה את אותה טעות?

    מקורות:

  • הקמצן שהפך לנדיב

    מר ג'ספר בוליין היה אחד מהקמצנים הבודדים שהפכו מודעים לחובתם כלפי אחיהם פחות ברי המזל. בלילה גורלי אחד הוא ספר את הונו המצטבר, והחליט לחלק אותו לנזקקים הראויים.

    הוא גילה שאם יחלק את אותו מספר ליש"ט מדי יום בשנה, הוא יוכל לחלק את כולו בדיוק על פני שנה שלמה מבלי שיישאר עודף; אבל אם ינוח בימי ראשון, ויחלק רק מספר קבוע של ליש"ט בכל יום חול, יישאר סובריין אחד בערב השנה החדשה. עכשיו, אם נניח את הסכום הנמוך ביותר האפשרי, מה היה הסכום המדויק של הליש"ט שהיה עליו לחלק?

    האם יכולה להיות שאלה פשוטה יותר? סכום של ליש"ט המחולק במספר ימים אחד אינו משאיר שארית, אך המחולק במספר ימים אחר משאיר סובריין אחד. זה הכל; ובכל זאת, כשאתם ניגשים לשאלה הקטנה הזו, תופתעו מכך שהיא יכולה להיות כל כך מבלבלת.

    מקורות:

  • בעיית גדר

    התועלת המעשית של חידות היא נקודה שאנו עלולים להתעלם ממנה. עם זאת, למעשה, מדי פעם קיבלתי מספר רב למדי של מכתבים מאנשים שמצאו שהשתלטות על עיקרון קטן שעליו נבנתה חידה, הוכיחה את עצמה כבעלת ערך רב עבורם בצורה בלתי צפויה ביותר. אכן, ניתן לקבל כעיקרון טוב שלחידה יש ערך מועט אמיתי אלא אם כן, בנוסף להיותה משעשעת ומבלבלת, היא מסתירה איזו תכונה מועילה ואולי מועילה. עם זאת, זה מאוד מוזר איך פיסות ידע נרכש קטנות אלה משתלבות בדרישות המזדמנות של חיי היומיום, ומוזר באותה מידה לאילו שימושים מוזרים ומסתוריים חלק מהקוראים שלנו נראים כמיישמים אותם. מה, למשל, יכול להיות המטרה של מר Wm. אוקסלי, שכותב לי מכל הדרך מאיווה, בבקשה לברר את ממדי השדה שהוא מציע לגדר, המכיל בדיוק את אותו מספר דונמים כמו שיש מעקות בגדר? האיש רוצה לגדר שדה מרובע לחלוטין שאמור להכיל בדיוק את אותו מספר דונמים כמו שיש מעקות בגדר הנדרשת. כל מכשול, או חלק מהגדר, הוא בגובה שבעה מעקות, ושני אורכים ימתחו מוט אחד (`16`½ רגל): כלומר, ישנם ארבעה עשר מעקות למוט, מידה קווית. עכשיו, מה צריך להיות גודל השדה? מקורות:

  • הקפת הריבועים

     

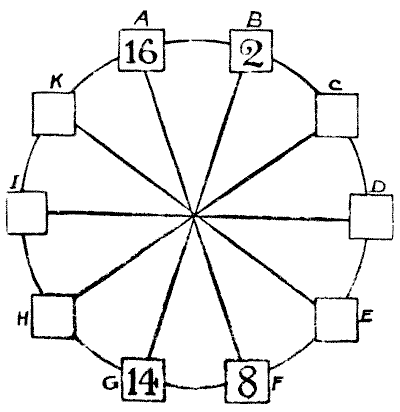
    החידה היא להציב מספר שונה בכל אחד מעשרת הריבועים כך שסכום ריבועי כל שני מספרים סמוכים יהיה שווה לסכום ריבועי שני המספרים הנמצאים בדיוק מולם במעגל. ארבעת המספרים המוצבים כדוגמאות חייבים להישאר במקומם. ריבוע של `16` הוא `256`, וריבוע של `2` הוא `4`. חברו אותם יחד, והתוצאה היא `260`. כמו כן—ריבוע של `14` הוא `196`, וריבוע של `8` הוא `64`. גם אלה יחד יוצרים `260`. עכשיו, באותו אופן בדיוק, B ו-C צריכים להיות שווים ל-G ו-H (הסכום לא בהכרח יהיה `260`), A ו-K ל-F ו-E, H ו-I ל-C ו-D, וכן הלאה, עם כל שני ריבועים סמוכים במעגל.

    כל שעליכם לעשות הוא למלא את ששת המספרים הנותרים. שברים אינם מותרים, ואני אראה שאף מספר לא צריך להכיל יותר משתי ספרות.

    מקורות:

  • ההפסד הקטן של ראקבריין

    הפרופסור ראקבריין בילה ערב עם חבריו הוותיקים, מר וגברת פוטס, והם שיחקו במשחק כלשהו (הוא לא מציין איזה משחק) קלפים. הפרופסור הפסיד במשחק הראשון, מה שהביא להכפלת הכסף שהונח על השולחן על ידי מר וגברת פוטס. את המשחק השני הפסידה גברת פוטס, מה שהכפיל את הכסף שהיה אז לבעלה ולפרופסור. באופן מוזר למדי, את המשחק השלישי הפסיד מר פוטס, והייתה לכך השפעה של הכפלת הכסף שהיה אז לאשתו ולפרופסור. לאחר מכן התברר שלכל אחד מהם היה בדיוק אותו סכום כסף, אך הפרופסור הפסיד חמישה שילינגים במהלך המשחק. כעת, שואל הפרופסור, מה היה סכום הכסף איתו הוא התיישב לשולחן? האם תוכלו לומר לו? מקורות:

  • החקלאי והכבשים שלו

     

    לחקלאי לונגמור הייתה נטייה מוזרה לחשבון, והוא היה ידוע באזורו כ"חקלאי המתמטי". הכומר החדש לא היה מודע לעובדה זו כשפגש את אחד מבני קהילתו בדרך, ושאל אותו במהלך שיחה קצרה, "ובכן, כמה כבשים יש לך בסך הכל?" לכן הוא הופתע למדי מתשובתו של לונגמור, שהייתה כדלקמן: "אתה יכול לחלק את הכבשים שלי לשני חלקים שונים, כך שההפרש בין שני המספרים יהיה זהה להפרש בין הריבועים שלהם. אולי, כבוד הכומר, תרצה לפתור את הסכום הקטן בעצמך."

    האם הקורא יכול לומר בדיוק כמה כבשים היו לחקלאי? נניח שהיו לו רק עשרים כבשים, והוא חילק אותן לשני החלקים `12` ו-`8`. עכשיו, ההפרש בין הריבועים שלהם, `144` ו-`64`, הוא `80`. אז זה לא יתאים, כי `4` ו-`80` בהחלט לא זהים. אם אתה יכול למצוא מספרים שמסתדרים נכון, תדע בדיוק כמה כבשים היו בבעלותו של החקלאי לונגמור.

    מקורות:

  • עץ או פלי

    קרוקס, מהמר כפייתי, אמר לאחרונה לחבר בגודווד, "אני מתערב איתך על חצי מהכסף שבכיסי על הטלת מטבע - אם ייצא עץ אני מנצח, אם ייצא פלי אני מפסיד." המטבע הוטל והכסף הועבר. הוא חזר על ההצעה שוב ושוב, בכל פעם הימר על חצי מהכסף שהיה ברשותו באותו רגע. לא נאמר לנו כמה זמן המשחק נמשך, או כמה פעמים הוטל המטבע, אבל אנחנו יודעים שמספר הפעמים שקרוקס הפסיד היה שווה בדיוק למספר הפעמים שהוא ניצח. האם הוא הרוויח או הפסיד מההרפתקה הקטנה הזו? מקורות:

  • חידת הנדנדה

    הצורך הוא אכן אם ההמצאה. נהניתי מאוד אתמול כשצפיתי בילד שרצה לשחק בנדנדה, ובשל כישלונו למצוא ילד אחר שיחלוק איתו את המשחק, הוא נאלץ לחזור אל הפתרון הגאוני של קשירת מספר לבנים לקצה אחד של הקרש כדי לאזן את משקלו בקצה השני.

    למעשה, הוא בדיוק התאזן מול שש-עשרה לבנים, כאשר אלה היו מחוברות לקצה הקצר של הקרש, אבל אם הוא חיבר אותן לקצה הארוך של הקרש הוא היה צריך רק אחת-עשרה לבנים כדי להתאזן.

    עכשיו, מה היה משקלו של הילד, אם לבנה שוקלת משקל שווה לשלושה רבעים של לבנה ושלושה רבעים של פאונד?

    מקורות: