אלגברה

אלגברה היא ענף רחב במתמטיקה המשתמש בסמלים (בדרך כלל אותיות) לייצוג מספרים ולהצגת כללים ויחסים. היא כוללת מניפולציה של ביטויים, פתרון משוואות ואי-שוויונים, וחקר פונקציות ומבנים. שאלות מכסות מגוון רחב של נושאים אלו.

טכניקה אלגברית משוואות אי שוויונים בעיות מילוליות סדרות

  • חידת חבל הכביסה

    ילד קשר חבל כביסה מראש כל אחד משני עמודים לבסיס של השני. לאחר מכן הוא הציע לאביו את השאלה הבאה. אם עמוד אחד היה בדיוק שבעה רגל מעל הקרקע והשני בדיוק חמישה רגל, מה היה הגובה מהקרקע שבו שני החבלים הצטלבו זה בזה? מקורות:

  • חידת הירח

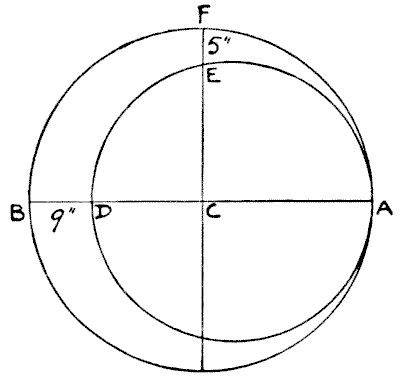    הנה חידה גיאומטרית קלה. הירח נוצר על ידי שני מעגלים, ו-C הוא מרכז המעגל הגדול יותר. רוחב הירח בין B ל-D הוא `9` אינץ', ובין E ל-F הוא `5` אינץ'. מהם הקטרים של שני המעגלים? מקורות:

  • הגן של ליידי בלינדה

    ליידי בלינדה היא גננת נלהבת. באיור היא מתוארת כשהיא שקועה בפתרון בעיה קטנה ומהנה שאותה אספר. אחד הגנים שלה הוא בצורת מלבן, מוקף בגדר חיה גבוהה של צמח ההולי, והיא הופכת אותו לגינת ורדים לטיפוח כמה מזני הורדים המשובחים ביותר שלה. היא רוצה להקדיש בדיוק מחצית משטח הגן לפרחים, בערוגה גדולה אחת, ואת המחצית השנייה לשביל המקיף אותו מכל צדדיו ברוחב שווה. גן כזה מוצג בתרשים בתחתית התמונה. כיצד עליה לסמן את הגן בתנאים פשוטים אלה? יש לה רק סרט מדידה, באורך הגן, כדי לעשות זאת, ומכיוון שגדר ההולי עבה וצפופה מאוד, עליה לבצע את כל המדידות בפנים. ליידי בלינדה לא ידעה את המידות המדויקות של הגן, ומכיוון שלא היה צורך שתדע, גם אני לא מציין מידות. זו משימה פשוטה למדי, לא משנה מה גודל או פרופורציות הגן. עם זאת, כמה גננות היו יודעות בדיוק כיצד להמשיך? סרט המדידה יכול להיות פשוט למדי - כלומר, אין צורך שיהיה מדד מדורג. מקורות:

  • חידה על עפיפון

    בעודי מלווה את ידידי, פרופסור הייפלייט, בתחרות הטסת עפיפונים מדעית בגבעות הדרומיות של סאסקס, נקלעתי לחישוב קטן שאמור לעניין את קוראיי. הפרופסור פרש את החוט שאליו היה מחובר העפיפון שלו מכננת שעליה הוא גולגל בצורה כדורית לחלוטין. כדור חוט זה היה בדיוק שני רגל בקוטר, ולחוט היה קוטר של מאיות אינץ'. מה היה אורך החוט?

    עכשיו, שאלה קטנה ופשוטה כזו שכולם יכולים להבין לחלוטין תגרום לרבים להתקשות לענות בכל דרך שהיא. בואו נראה אם, מבלי להיכנס לחישובים מתמטיים מעמיקים כלשהם, נוכל לקבל את התשובה בערך - נניח, בטווח של מייל אחד ממה שנכון! נניח שכאשר החוט מגולגל כולו הכדור מוצק לחלוטין לכל אורכו, ואין צורך להתחשב בציר שעובר דרכו. עם הפשטה זו, אני תוהה כמה קוראים יכולים לציין אפילו בטווח של מייל אחד מהתשובה הנכונה את אורך החוט הזה.

    מקורות:

  • איך ליצור בורות מים

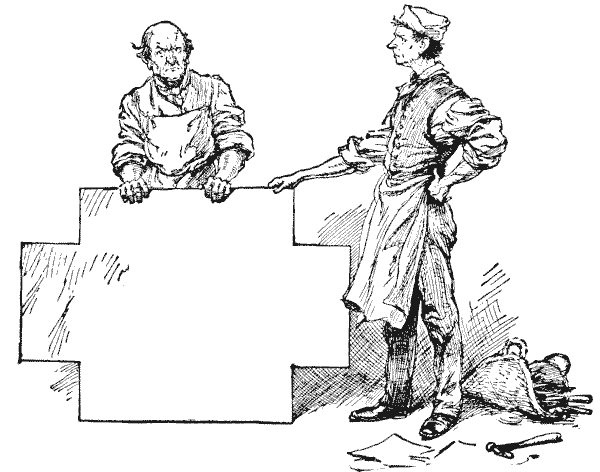    לידידנו באיור יש יריעת אבץ גדולה, שממדיה (לפני החיתוך) שמונה רגל על שלוש רגל, והוא חתך פיסות מרובעות (כולן באותו גודל) מארבע הפינות וכעת הוא מציע לקפל את הצדדים, להלחים את הקצוות, ולהכין בור מים. אבל הנקודה שמבלבלת אותו היא זו: האם הוא חתך את פיסות הריבוע בגודל הנכון, כך שהבור יכיל את הכמות הגדולה ביותר האפשרית של מים? אתם רואים, אם חותכים אותם קטנים מאוד, מקבלים בור רדוד מאוד; אם חותכים אותם גדולים, מקבלים בור גבוה וצר. הכל עניין של למצוא דרך לחתוך את ארבע פיסות הריבוע האלה בדיוק בגודל הנכון. איך נוכל להימנע מלחתוך אותם קטנים מדי או גדולים מדי? מקורות:

  • שש הצפרדעים

    שש הצפרדעים המשכילות באיור אומנו להפוך את סדרן, כך שהמספרים שלהן יהיו `6, 5, 4, 3, 2, 1`, כאשר הריבוע הריק נמצא במיקומו הנוכחי. הן יכולות לקפוץ למשבצת הבאה (אם היא פנויה) או לדלג מעל צפרדע אחת למשבצת הבאה מעבר לה (אם היא פנויה), בדיוק כפי שאנו נעים במשחק הדמקה, ויכולות לנוע אחורה או קדימה כרצונן. האם תוכלו להראות כיצד הן מבצעות את המשימה שלהן במספר המהלכים המועט ביותר האפשרי? זה די קל, אז כשסיימתם הוסיפו צפרדע שביעית מימין ונסו שוב. לאחר מכן הוסיפו עוד צפרדעים עד שתוכלו לתת את הפתרון הקצר ביותר עבור כל מספר. כי זה תמיד אפשרי, עם המשבצת הריקה הבודדת הזו, לא משנה כמה צפרדעים יש. מקורות:

  • חֲמֵשׁ עֶשְׂרֵה כְּבָשִׂים

    אנציקלופדיה מסוימת הציגה את הבעיה המוזרה הבאה, כך שמעתי: "הנח חמש עשרה כבשים בארבעה מכלאות כך שיהיה אותו מספר כבשים בכל מכלאה." לא ניתנה תשובה כלשהי, אז החלטתי לחקור את הנושא. ראיתי שבהתמודדות עם תפוחים או לבנים, הדבר ייראה בלתי אפשרי לחלוטין, מכיוון שארבע פעמים כל מספר חייב להיות מספר זוגי, בעוד שחמש עשרה הוא מספר אי-זוגי. לכן חשבתי שחייבת להיות תכונה מסוימת לכבשים שלא הייתה ידועה בדרך כלל. אז החלטתי לראיין כמה חקלאים בנושא. הראשון ציין שאם נכניס מכלאה אחת בתוך השנייה, כמו הטבעות של מטרה, ונניח את כל הכבשים במכלאה הקטנה ביותר, הכל יהיה בסדר. אבל התנגדתי לכך, כי אתה מודה שאתה מניח את כל הכבשים במכלאה אחת, לא בארבע מכלאות. האיש השני אמר שאם אני אניח ארבע כבשים בכל אחת משלוש מכלאות ושלוש כבשים במכלאה האחרונה (כלומר חמש עשרה כבשים בסך הכל), ולאחת הכבשות במכלאה האחרונה יהיה טלה במהלך הלילה, יהיה אותו מספר בכל מכלאה בבוקר. גם זה לא סיפק אותי. החקלאי השלישי אמר, "יש לי ארבע מכלאות גדר בשדה שלי, ועדר קטן של כבשים מסורסים, אז אם רק תרד איתי למטה אני אראה לך איך זה נעשה." האיור מתאר את ידידי כשהוא עומד להדגים לי את העניין. ההסבר הבהיר שלו היה כנראה זה שהיה במוחו של כותב המאמר באנציקלופדיה. מה זה היה? האם אתה יכול להניח את חמש עשרה הכבשים האלה? מקורות:

  • חידת מעונות

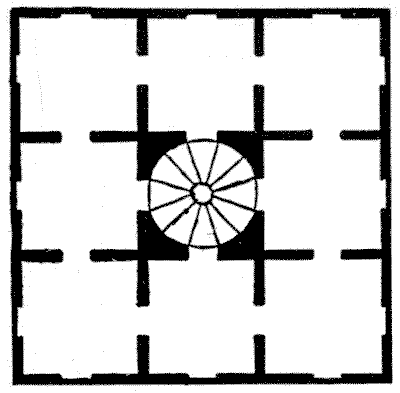
    במנזר מסוים היו שמונה מעונות גדולים בקומה אחת, שאליהם הגיעה גרם מדרגות ספירלי במרכז, כפי שמוצג בתרשים שלנו. בבדיקה שערכה אם המנזר ביום שני אחד, התגלה שהצד הדרומי מועדף כל כך, שפי שישה נזירות ישנו בצד הדרומי מאשר בכל אחד משלושת הצדדים האחרים. היא התנגדה לצפיפות היתר הזו, והורתה לצמצם אותה. ביום שלישי היא גילתה שפי חמש נזירות ישנו בצד הדרומי מאשר בכל אחד מהצדדים האחרים. שוב היא התלוננה. ביום רביעי היא מצאה פי ארבעה בצד הדרומי, ביום חמישי פי שלושה, וביום שישי פי שניים. לאחר שהאיצה בנזירות להמשיך במאמצים, היא שמחה לגלות ביום שבת שמספר שווה ישן בכל אחד מארבעת צדי הבית. מהו המספר הקטן ביותר של נזירות שיכול היה להיות שם, וכיצד הן יכלו להסתדר בכל אחד מששת הלילות? אסור שאף חדר יהיה ריק.

    מקורות:

  • קערת הוואסייל

    בערב חג המולד אחד, שלושה וילי עייפים השיגו את מה שהיה עבורם כמו קערת וואסייל של ממש, בצורה של חבית קטנה, שהכילה בדיוק שישה ליטרים של בירה משובחת. לאחד האנשים היה כד של חמישה פינטים ולאחר כד של שלושה פינטים, והבעיה שלהם הייתה לחלק את המשקה שווה בשווה ביניהם בלי בזבוז. כמובן, אסור להם להשתמש בכלים או מידות אחרות. אם אתה יכול להראות איך זה נעשה בכלל, אז נסה למצוא את הדרך הדורשת את מספר המניפולציות המינימלי האפשרי, כאשר כל מזיגה נפרדת מכלי אחד למשנהו, או לגרונו של אדם, נחשבת כמניפולציה.

    מקורות:

  • השאלה של הדוקטור

    "נקודה קטנה ומסקרנת עלתה בדעתי במרפאה שלי הבוקר", אמר רופא. "הייתה לי בקבוק שהכיל עשרה אונקיות של כוהל, ובקבוק אחר שהכיל עשרה אונקיות של מים. מזגתי רבע אונקיה של כוהל לתוך המים וניערתי אותם יחד. התערובת הייתה אז בבירור ארבעים לאחד. אחר כך מזגתי חזרה רבע אונקיה מהתערובת, כך ששני הבקבוקים יכילו שוב כל אחד את אותה כמות נוזל. מה היה היחס בין כוהל למים שהכיל בקבוק הכוהל אז?" מקורות: