אלגברה

אלגברה היא ענף רחב במתמטיקה המשתמש בסמלים (בדרך כלל אותיות) לייצוג מספרים ולהצגת כללים ויחסים. היא כוללת מניפולציה של ביטויים, פתרון משוואות ואי-שוויונים, וחקר פונקציות ומבנים. שאלות מכסות מגוון רחב של נושאים אלו.

טכניקה אלגברית משוואות אי שוויונים בעיות מילוליות סדרות

  • דומינו בסדרה

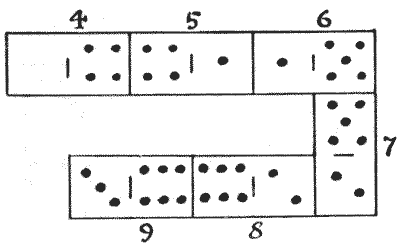    ניתן לראות ששיחקתי שישה אבני דומינו, באיור, בהתאם לכללים הרגילים של המשחק, `4` נגד `4, 1` נגד `1`, וכן הלאה, ועדיין סכום הנקודות על אבני הדומינו העוקבות, `4, 5, 6, 7, 8, 9`, נמצא בסדרה חשבונית; כלומר, למספרים שנלקחו לפי הסדר יש הפרש קבוע של `1`. בכמה דרכים שונות נוכל לשחק שישה אבני דומינו, מקופסה רגילה של עשרים ושמונה, כך שהמספרים עליהם יהיו בסדרה חשבונית? אנחנו תמיד חייבים לשחק משמאל לימין, ומספרים בסדרה חשבונית יורדת (כגון `9, 8, 7, 6, 5, 4`) אינם קבילים. מקורות:

  • פאזל מסגרת הקלפים

    באיור יש לנו מסגרת הבנויה מעשרה קלפי משחק, אס עד עשר יהלום. הילדים שהכינו אותה רצו שהנקודות ניקוד בכל ארבעת הצדדים יסתכמו באופן שווה, אבל הם נכשלו בניסיונם וויתרו עליה כבלתי אפשרית. ניתן לראות שהנקודות בשורה העליונה, בשורה התחתונה ובצד שמאל מסתכמות כולן ב-`14`, אבל הצד הימני מסתכם ב-`23`. עכשיו, מה שהם ניסו לעשות הוא די אפשרי. האם אתה יכול לסדר מחדש את עשרת הקלפים באותה תצורה כך שכל ארבעת הצדדים יסתכמו באופן שווה? כמובן שהם לא צריכים להסתכם ב-`14`, אלא בכל מספר שתבחר.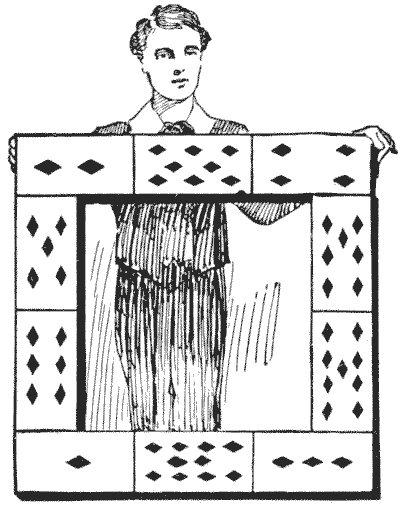 מקורות:

  • טריק עם קוביות

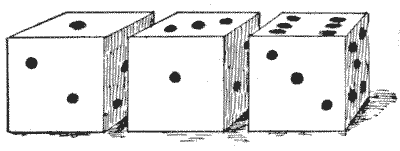    הנה טריק קטן ונחמד עם שלוש קוביות. אני מבקש ממך לזרוק את הקוביות מבלי שאראה אותן. לאחר מכן אני אומר לך להכפיל את הנקודות של הקוביה הראשונה ב-`2` ולהוסיף `5`; ואז להכפיל את התוצאה ב-`5` ולהוסיף את הנקודות של הקוביה השנייה; ואז להכפיל את התוצאה ב-`10` ולהוסיף את הנקודות של הקוביה השלישית. לאחר מכן אתה נותן לי את הסכום הכולל, ואני יכול מיד לומר לך את הנקודות שנזרקו בשלוש הקוביות. איך אני עושה את זה? לדוגמה, אם זרקת `1, 3`, ו-`6`, כפי שמוצג באיור, התוצאה שהיית נותן לי תהיה `386`, שממנה אוכל מיד לומר מה זרקת. מקורות:

  • משחק קריקט בכפר

    במשחק קריקט, Dingley Dell v. All Muggleton, האחרון קיבל את הסיבוב הראשון. מר דמפקינס ומר פודר היו בשערים, כאשר דמפקינס הזהיר ביצע חיתוך מאוחר מרהיב, ומר פודר קרא לו לרוץ. ארבע ריצות הושלמו לכאורה, אך השופטים הערניים בכל קצה קראו, "שלוש חסרות," מה שהפך לשש ריצות חסרות בסך הכל. איזה מספר השיג מר דמפקינס? כאשר Dingley Dell קיבלו את תורם בשערים, האלופים שלהם היו מר לאפי ומר סטראגלס. האחרון ביצע נסיעה מרהיבה מהצד, והזמין את עמיתו "לבוא," וכתוצאה מכך הצופים הבחינו ומחאו כפיים על מה שהיה אמור להיות שלוש ריצות חדות. אבל השופטים הצהירו שהיו שתי ריצות חסרות בכל קצה - ארבע בסך הכל. באיזו מידה, אם בכלל, התמרון הזה הגדיל את סך הנקודות של מר סטראגלס? מקורות:

  • צרצר איטי

    במשחק המחוז האחרון בין ווסקס לנינקומשייר, הקבוצה הראשונה הייתה על המגרש כל היום, השחקן האחרון הוצא כמה דקות לפני הזמן לסיום המשחק. המשחק היה כל כך איטי שרוב הצופים נרדמו עמוק, וכשהתעוררו על ידי אחד הפקידים שפינה את השטח, למדנו ששני שחקנים הוצאו בפסיקה לג-בפור-וויקט עם ציון משולב של `19` ריצות; ארבעה שחקנים נתפסו עם ציון משולב של `17` ריצות; שחקן אחד הודח בריצה עם ניקוד אפס; והשאר הודחו באמצעות באולינג עבור `3` ריצות כל אחד. לא היו תוספות. לא נאמר לנו מי מהשחקנים היה הקפטן, אבל הוא השיג בדיוק `15` יותר מהממוצע של הקבוצה שלו. מה היה הניקוד של הקפטן? מקורות:

  • חידת מרוץ הסוסים

    אין מוסר בחידות. כאשר אנו פותרים את החידה הישנה על הקברניט שנאלץ להשליך חצי מצוותו מעבר לסיפון בסערה, והסכים לערוך הגרלה, אך סידר את האנשים כך שרק הטורקים הוקרבו, וכל הנוצרים נותרו על הסיפון, איננו עוצרים לדון במוסריות המפוקפקת של ההליך. וכאשר אנו עוסקים בבעיית מדידה, שבה צליינים צמאים מסוימים אמורים לערוך חלוקה הוגנת של חבית בירה, איננו מתנגדים לכך, כמנועים מוחלטים, שזה מנוגד למצפוננו להתעסק עם משקאות משכרים. לכן איני מתנצל על הצגת חידה העוסקת בהימורים.

    שלושה סוסים—בלוט, כחול-בקבוק וקפסולה—מתחילים במרוץ. יחסי ההימורים הם `4` ל-`1`, בלוט; `3` ל-`1`, כחול-בקבוק; `2` ל-`1`, קפסולה. עכשיו, כמה עלי להשקיע על כל סוס כדי לזכות ב-£`13`, לא משנה איזה סוס יגיע ראשון? נניח, לדוגמה, שהימרתי £`5` על כל סוס. אז, אם בלוט ינצח, אקבל £`20` (ארבע פעמים £`5`), ואצטרך לשלם £`5` עבור כל אחד משני הסוסים האחרים; ובכך אזכה ב-£`10`. אבל יתברר שאם כחול-בקבוק יהיה ראשון אזכה רק ב-£`5`, ואם קפסולה תנצח לא ארוויח דבר ולא אפסיד דבר. זה יבהיר את השאלה לחלוטין למתחילים, שכמוני, לא מתעניינים בקריאה של האחווה שמצהירה שהיא עוסקת במשימה הנאצלת של "שיפור גזע הסוסים".

    מקורות:

  • מרוץ המכוניות

    לפעמים הצהרה פשוטה למדי, אם מנוסחת באופן לא מוכר, תגרום למבוכה ניכרת. הנה דוגמה, וללא ספק היא תבלבל קצת את חלק מקוראי הצעירים יותר שלי. במקרה הייתי במרוץ מכוניות בברוקלנדס, כשצופה אחד אמר למשנהו, בזמן שמספר מכוניות הסתובבו סביב המסלול המעגלי:—

    "הנה גוגלסמית'—האיש הזה במכונית הלבנה!"

    "כן, אני רואה," הייתה התשובה; "אבל כמה מכוניות רצות במרוץ הזה?"

    אז באה התשובה המוזרה הזו:—

    "שליש מהמכוניות שלפני גוגלסמית' ועוד שלושה רבעים מאלה שמאחוריו יתנו לך את התשובה."

    עכשיו, האם אתה יכול לומר כמה מכוניות רצו במרוץ?

    מקורות:

  • הצינוק הספרדי

    לא רחוק מחמישים מייל מקדיז ניצב בימי הביניים מבצר, שכל עקבותיו נעלמו במשך מאות שנים. בין שאר המאפיינים המעניינים, המבצר הזה הכיל צינוק לא נעים במיוחד, המחולק לשישה עשר תאים, כולם מתקשרים זה עם זה, כפי שמוצג באיור.

    עתה, המושל היה עליז, וחובב חידות גדול. יום אחד הוא הלך לצינוק ואמר לאסירים, "בחיי!" (או המקבילה שלו בספרדית) "כולכם תשוחררו אם תוכלו לפתור את החידה הזו. עליכם לסדר את עצמכם בשישה עשר התאים כך שהמספרים על גבכם יהוו ריבוע קסם שבו כל טור, כל שורה וכל אחד משני האלכסונים יסתכמו לאותו מספר. רק זכרו זאת: שאף אחד מכם לא יהיה ביחד באותו תא."

    אחד האסירים, לאחר שעבד על הבעיה במשך יומיים או שלושה, עם חתיכת גיר, לקח על עצמו להשיג את חירותו וחירות חבריו האסירים אם הם ילכו בעקבות הוראותיו ויעברו דרך הפתח מתא לתא בסדר שבו יקרא את המספרים שלהם. 

     

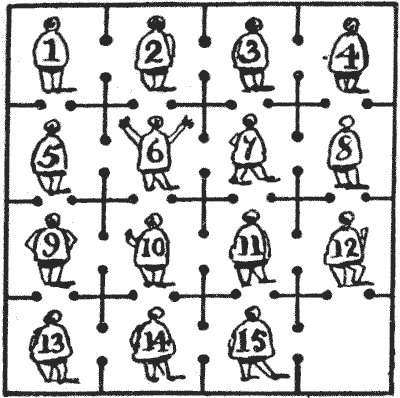
    הוא הצליח בניסיונו, ומה שמרשים יותר, כך נראה מהתיאור של שיטתו שנרשם בכתב היד העתיק שלפניי, שהוא עשה זאת במספר המהלכים המועט ביותר האפשרי. הקורא מתבקש להראות מה היו המהלכים האלה.

    מקורות:

  • טבעות הברזל המייגעות

     

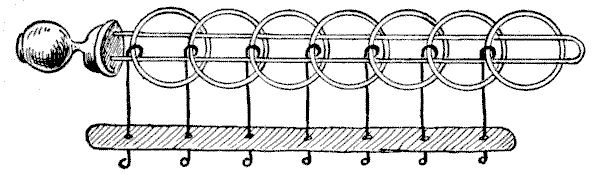
    האיור מייצג אחד מהחידות המכאניות העתיקות ביותר. מקורו אינו ידוע. קרדנו, המתמטיקאי, כתב עליו בשנת `1550`, וואליס בשנת `1693`; בעוד שאומרים שהוא עדיין נמצא בכפרים אנגליים נידחים (לפעמים מונח במקומות מוזרים, כמו מגדל פעמונים של כנסייה), עשוי מברזל, ונקרא באופן הולם "טבעות מייגעות", ומשמש את הנורווגים כיום כמנעול לקופסאות ותיקים. בחנויות הצעצועים הוא נקרא לפעמים "טבעות סיניות", אם כי נראה שאין סמכות לתיאור, ולרוב הוא מכונה בשם הלא מספק "הטבעות המבלבלות". הצרפתים קוראים לזה "Baguenaudier."

    ניתן לראות שהחידה מורכבת מ-לולאה פשוטה של חוט המקובעת בידית שאותה מחזיקים ביד שמאל, וממספר מסוים של טבעות המאובטחות על ידי חוטים העוברים דרך חורים ב-מוט ונשמרים שם על ידי קצותיהם הקהים. החוטים פועלים בחופשיות במוט, אך אינם יכולים להיפרד ממנו, וגם לא ניתן להסיר את החוטים מהטבעות. החידה הכללית היא לנתק את הלולאה לחלוטין מכל הטבעות, ואז להחזיר את כולן שוב.

    כעת, ניתן לראות במבט חטוף שניתן להסיר את הטבעת הראשונה (מימין) בכל עת על ידי החלקתה מעל הקצה והשלכתה דרך הלולאה; או שאפשר להחזיר אותה על ידי היפוך הפעולה. מלבד זאת, הטבעת היחידה שניתן להסיר אי פעם היא זו שבמקרה נמצאת השנייה הסמוכה על הלולאה בקצה הימני. כך, כשכל הטבעות עליה, ניתן להפיל את השנייה מיד; כשהטבעת הראשונה למטה, אינך יכול להפיל את השנייה, אך תוכל להסיר את השלישית; כששלוש הטבעות הראשונות למטה, אינך יכול להפיל את הרביעית, אך תוכל להסיר את החמישית; וכן הלאה. יתברר שאפשר להפיל את הטבעות הראשונה והשנייה יחד או להחזיר אותן יחד; אך כדי למנוע בלבול, לא נאפשר את המהלך הכפול החריג הזה, ונגיד שניתן להחזיר או להסיר רק טבעת אחת בכל פעם.

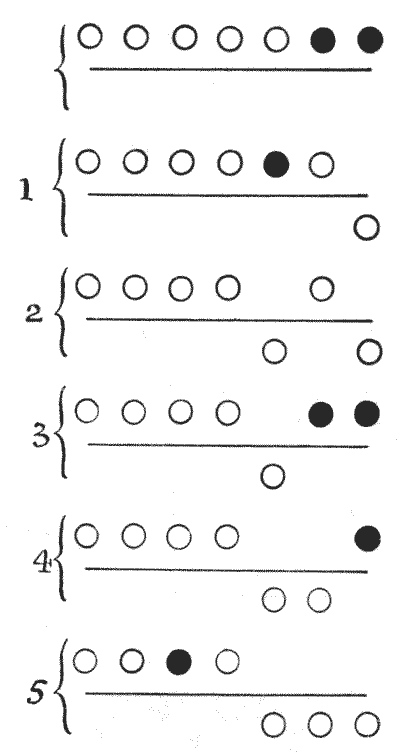
    אנו יכולים להסיר טבעת אחת ב-`1` מהלך; שתי טבעות ב-`2` מהלכים; שלוש טבעות ב-`5` מהלכים; ארבע טבעות ב-`10` מהלכים; חמש טבעות ב-`21` מהלכים; ואם נמשיך להכפיל (ולהוסיף אחד כאשר מספר הטבעות הוא אי-זוגי) נוכל לברר בקלות את מספר המהלכים להסרת כל מספר טבעות לחלוטין. כדי להוריד את כל שבע הטבעות נדרשים `85` מהלכים. בואו נסתכל על חמשת המהלכים שנעשו בהסרת שלוש הטבעות הראשונות, העיגולים מעל הקו מייצגים טבעות על הלולאה ואלה שמתחת מייצגים טבעות מחוץ ללולאה.

    הפילו את הטבעת הראשונה; הפילו את השלישית; הרימו את הראשונה; הפילו את השנייה; והפילו את הראשונה—`5` מהלכים, כפי שמוצג בבירור בתרשימים. העיגולים הכהים מראים בכל שלב, ממצב ההתחלה ועד הסיום, אילו טבעות אפשר להפיל. לאחר מהלך `2` יורגש שלא ניתן להפיל אף טבעת עד שאחת תוחזר, מכיוון שהטבעות הראשונה והשנייה מימין שנמצאות כעת על הלולאה אינן יחד. לאחר המהלך החמישי, אם ברצוננו להסיר את כל שבע הטבעות, עלינו כעת להפיל את החמישית. אבל לפני שנוכל להסיר אז את הרביעית, יש צורך להחזיר את שלוש הראשונות ולהסיר את שתי הראשונות. אז יהיו לנו `7, 6, 4, 3` על הלולאה, ולכן נוכל להפיל את הרביעית. כשנחזיר `2` ו-`1` ונסיר `3, 2, 1`, נוכל להפיל את הטבעת השביעית. הפעולה הבאה אז תהיה להשיג `6, 5, 4, 3, 2, 1` על הלולאה ולהסיר `4, 3, 2, 1`, ואז `6` תרד; ואז להשיג `5, 4, 3, 2, 1` על הלולאה, ולהסיר `3, 2, 1`, ואז `5` תרד; ואז להשיג `4, 3, 2, 1` על הלולאה ולהסיר `2, 1`, ואז `4` תרד; ואז להשיג `3, 2, 1` על הלולאה ולהסיר `1`, ואז `3` תרד; ואז להשיג `2, 1` על הלולאה, ואז `2` תרד; ו-`1` תיפול דרך במהלך ה-85, ותשאיר את הלולאה חופשית לחלוטין. על הקורא להיות מסוגל כעת להבין את החידה, בין אם יש לו אותה ביד בצורה מעשית ובין אם לא.

     

    הבעיה המסוימת שאני מציע היא פשוט זו. נניח שיש בסך הכל ארבע עשרה טבעות על טבעות הברזל המייגעות, ואנו ממשיכים להסיר את כולן בצורה הנכונה כדי לא לבזבז אף מהלך. מה יהיה מצב הטבעות לאחר שבוצע המהלך ה-`9`,999?

    מקורות:

  • עלייה במדרגות כזו

    בווילה פרברית יש גרם מדרגות קטן עם שמונה מדרגות, לא כולל משטח הנחיתה. החידה הקטנה שבה טומי סמארט הדהים את משפחתו היא זו. עליכם להתחיל מלמטה ולנחות פעמיים על הרצפה מעל (ולעצור שם בסיום), לאחר שחזרתם פעם אחת לקומת הקרקע. אבל עליכם להקפיד להשתמש בכל מדרגה אותו מספר פעמים. בכמה צעדים מעטים תוכלו לבצע את העלייה? זה נראה עניין פשוט מאוד, אבל סביר להניח שבניסיון הראשון שלכם תעשו הרבה יותר צעדים מהנדרש. כמובן שאסור לכם לעלות יותר ממדרגה אחת בכל פעם.

    טומי מכיר את הטריק, והראה אותו לאביו, שמצהיר על בוז לדברים כאלה; אבל כשהילדים במיטה, האב לוקח לעתים קרובות חברים למסדרון ונהנה מצחוק טוב על הבלבול שלהם. ובכל זאת, הכל כל כך פשוט כשאתה יודע איך זה נעשה.

    מקורות: