אלגברה, סדרות

סדרה היא רשימה סדורה של מספרים (או פריטים אחרים) שלעיתים קרובות עוקבת אחר כלל או תבנית ספציפיים. נושא זה מכסה זיהוי תבניות, מציאת איברים ספציפיים, קביעת נוסחאות כלליות (האיבר ה-`n`-י), והבנת סוגים שונים של סדרות (חשבוניות, הנדסיות, רקורסיביות).

• הדילמה של אנשי הארטילריה

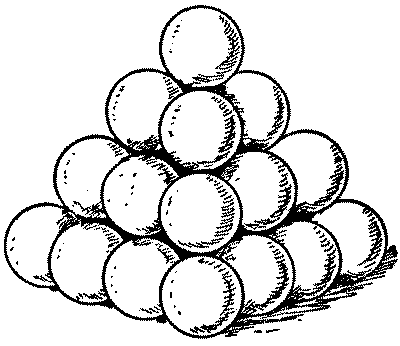  "יש לערום את כל כדורי התותח בפירמידות מרובעות," הייתה הפקודה שהוצאה לגדוד. כך נעשה. ואז הגיעה הפקודה הנוספת, "כל הפירמידות צריכות להכיל מספר ריבועי של כדורים." ואז החלו הצרות. "אי אפשר לעשות את זה," אמר המג'ור. "תסתכלו על הפירמידה הזו, למשל; יש שישה עשר כדורים בבסיס, אחר כך תשעה, אחר כך ארבעה, ואז אחד בקצה, מה שנותן שלושים כדורים בסך הכל. אבל חייבים להיות עוד שישה כדורים, או חמישה פחות, כדי ליצור מספר ריבועי." "חייבים לעשות את זה," התעקש הגנרל. "כל מה שאתם צריכים לעשות הוא לשים את המספר הנכון של כדורים בפירמידות שלכם." "הבנתי!" אמר סגן, הגאון המתמטי של הגדוד. "הניחו את הכדורים בנפרד." "שטויות!" קרא הגנרל. "אתה לא יכול לערם כדור אחד לפירמידה!" האם באמת אפשר לציית לשתי הפקודות?
  נושאים:

  אלגברה -> משוואות אלגברה -> סדרות תורת המספרים -> מספרים משולשיים
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 138

• חידת תפוח האדמה

  קחו פרוסה עגולה של תפוח אדמה, הניחו אותה על השולחן, ובדקו לכמה חלקים תוכלו לחלק אותה באמצעות שישה חיתוכים בסכין. כמובן שאסור לכם לסדר מחדש את החלקים או לערום אותם לאחר חיתוך. מהו המספר הגדול ביותר של חלקים שתוכלו ליצור?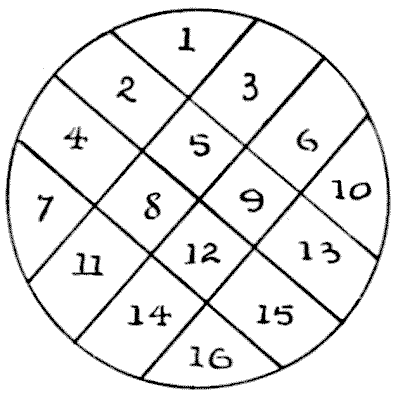 האיור מראה כיצד ליצור שישה עשר חלקים. כמובן שאפשר לשפר תוצאה זו בקלות.
  נושאים:

  גאומטריה -> גאומטריה במישור אלגברה -> סדרות קומבינטוריקה -> גאומטריה קומבינטורית -> חתכו צורה
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 164

• עלייה במדרגות כזו

  בווילה פרברית יש גרם מדרגות קטן עם שמונה מדרגות, לא כולל משטח הנחיתה. החידה הקטנה שבה טומי סמארט הדהים את משפחתו היא זו. עליכם להתחיל מלמטה ולנחות פעמיים על הרצפה מעל (ולעצור שם בסיום), לאחר שחזרתם פעם אחת לקומת הקרקע. אבל עליכם להקפיד להשתמש בכל מדרגה אותו מספר פעמים. בכמה צעדים מעטים תוכלו לבצע את העלייה? זה נראה עניין פשוט מאוד, אבל סביר להניח שבניסיון הראשון שלכם תעשו הרבה יותר צעדים מהנדרש. כמובן שאסור לכם לעלות יותר ממדרגה אחת בכל פעם.

  טומי מכיר את הטריק, והראה אותו לאביו, שמצהיר על בוז לדברים כאלה; אבל כשהילדים במיטה, האב לוקח לעתים קרובות חברים למסדרון ונהנה מצחוק טוב על הבלבול שלהם. ובכל זאת, הכל כל כך פשוט כשאתה יודע איך זה נעשה.

  נושאים:

  אריתמטיקה אלגברה -> בעיות מילוליות אלגברה -> סדרות
  מקורות:
  • שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 418

• המשיכו את הסדרה

  `2, 6, 12, 20, 30…`

  א. מה המספר הבא (השישי) בסדרה?

  ב. מה המספר ה-`2016` בסדרה?

  נושאים:

  אריתמטיקה לוגיקה -> הגיון אלגברה -> סדרות -> סדרה חשבונית אלגברה -> סדרות -> השלימו\המשיכו סדרה
  מקורות:
  • אתר האינטרנט problems.ru

• שאלה

  בהינתן מספר שלם חיובי N, נתבונן בתהליך הבא: נסמן ב-`S(N)` את סכום הספרות של N ניקח את סכום הספרות של `S(N)`  נחזור על הפעולה שוב ושוב עד שנקבל מספר חד ספרתי נקרא למספר הפעמים שביצענו את התהליך הנ"ל עד שקיבלנו מספר חד-ספרתי: "העומק" של N. לדוגמה, העומק של 49 הוא `S(49)=13 -> S(13)=4)2` , הפעולה בוצעה פעמיים( והעומק של 45 הוא 1.

  א) הוכיחו כי לכל מספר N אכן יש עומק סופי, כלומר, שתמיד יתקבל מספר חד-ספרתי בשלב כלשהו של התהליך.

  ב) נסמן ב-`x(n)` את המספר המינימלי (שערכו הקטן ביותר) בעל עומק N. מצאו את השארית של `x(5776)` בחילוק ב-6 .נמקו את תשובתכם!

  ג) מצאו את השארית של המספר `x(5776) - x(5708)` בחילוק ב-2016 .נמקו את תשובתכם!

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> חשבון השאריות קומבינטוריקה -> אינדוקציה אלגברה -> סדרות -> סדרה חשבונית
  מקורות:
  • אולימפיאדת גיליס, תשע"ו שאלה 3

• שאלה

  מצאו את המסכום של כל המספרים הטבעיים מ-`1` עד `100`.

  נושאים:

  אריתמטיקה אלגברה -> טכניקה אלגברית לוגיקה -> הגיון אלגברה -> סדרות -> סדרה חשבונית

• שאלה

  על הלוח כתובים המספרים: `1, 2, 3, …, 2016, 2017`. תוך מהלך אחד מותר לבחור זוג מספרים שכתובים על הלוח, למחוק אותם ולרשום במקומם את ההפרש שלהם (החיובי). אחרי מספר פעולות כאלו נשאר על הלוח מספר בודד. האם יתכן שזה אפס?

  נושאים:

  אריתמטיקה קומבינטוריקה -> אינווריאנטים קומבינטוריקה -> אינדוקציה תורת המספרים -> חלוקה -> זוגיות אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים הוכחה ודוגמה -> הוכחה בשלילה

• שאלה

  האם קיימת סדרה חשבונית אינסופית שמורכבת ממספרים ראשוניים בלבד?

  הערה: לא נתיחס לסדרות חשבוניות "טריוויאליות", שהן קבועות.

  הצגת רמז

  התחברו כאן לאתר על מנת לקבל את הרמז
  נושאים:

  תורת המספרים -> מספרים ראשוניים אלגברה -> סדרות -> סדרה חשבונית הוכחה ודוגמה -> הוכחה בשלילה

• שאלה

  בכמה סכום כל המספרים הזוגיים שלא עוברים את `100` גדול יותר מסכום כל המספרים האי זוגיים שלא עוברים את `100`?

  נושאים:

  אריתמטיקה קומבינטוריקה -> ספירה כפולה אלגברה -> טכניקה אלגברית לוגיקה -> הגיון אלגברה -> סדרות -> סדרה חשבונית

• שאלה

  הוכיחו כי 

  `1+3+5+...+(2n-1)=n^2`

  נושאים:

  קומבינטוריקה -> אינדוקציה אלגברה -> סדרות -> סדרה חשבונית