אלגברה, סדרות
סדרה היא רשימה סדורה של מספרים (או פריטים אחרים) שלעיתים קרובות עוקבת אחר כלל או תבנית ספציפיים. נושא זה מכסה זיהוי תבניות, מציאת איברים ספציפיים, קביעת נוסחאות כלליות (האיבר ה-`n`-י), והבנת סוגים שונים של סדרות (חשבוניות, הנדסיות, רקורסיביות).
סדרה חשבונית השלימו\המשיכו סדרה נוסחאות נסיגה-
מסגרת
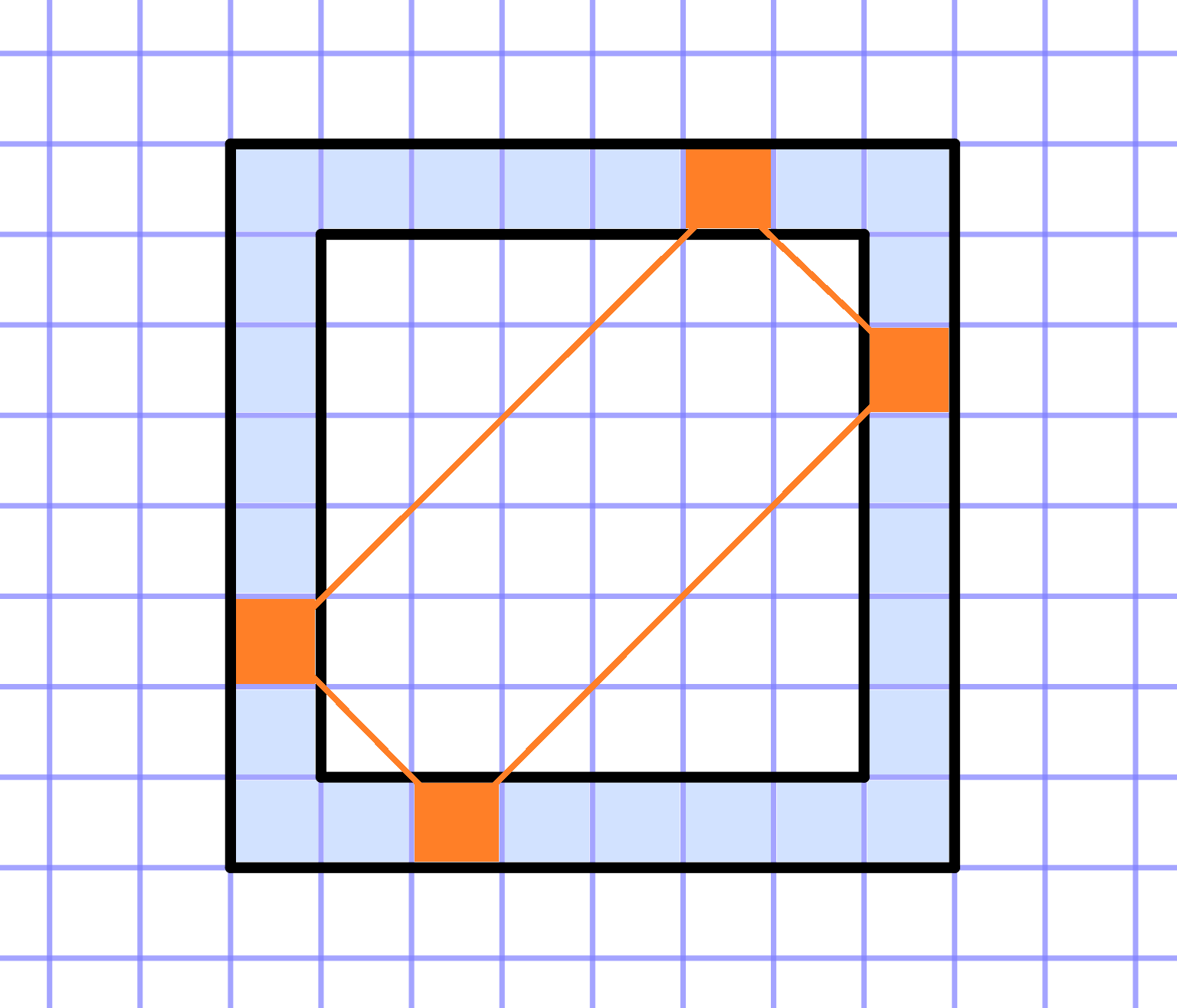
על דף משבצות נתון ריבוע בגודל `NxxN`. נתבנן במסגרת שלו בעובי של משבצת אחת. היא מורכבת מ-`4*(N-1)` משבצות.
האם תוכלו לרשום במשבצות של המסגרת `4*(N-1)` מספרים שלמים עוקבים (לא בהכרח חיוביים), כך שיתקיים התנאי הבא:
לכל מלבן שקודקודיו נמצאים על המסגרת וצלעותיו מקבילים לאלכסונים של הריבוע המקורי, סכום המספרים בקודקודים שווה לגודל קבוע. זה כולל גם את המלבנים "המנוונים" בעלי רוחב אפס שמתלכדים עם האלכסונים של הריבוע - במקרה הזה פשוט סוכמים את שני המספרים בקודקודים המנוגדים של הריבוע
עבור:
א. `N=3`
ב. `N=4`
ג. `N=5`
 מקורות:נושאים:אריתמטיקה תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים
מקורות:נושאים:אריתמטיקה תורת המספרים -> חלוקה -> זוגיות הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית קומבינטוריקה -> בדיקת מקרים -> תהליכים- תחרות הערים, תשמ"ד, סתיו, גרסת תרגול, כיתות ט-י שאלה 3 נקודות 2+3+4
-
שאלה
`120` כדורים זהים מונחים בצורה של פירמידה משולשת. כמה שכבות יש בפירמידה?
הערה: מדובר בפירמידה, שהיא צורה תלת מימדית, ולא במשולש במישור.
נושאים:גאומטריה -> גאומטריה במרחב אריתמטיקה לוגיקה -> הגיון הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית אלגברה -> סדרות -> השלימו\המשיכו סדרה תורת המספרים -> מספרים משולשיים -
שאלה
נתונה הסדרה `1 , 1/2 ,1/3 ,1/4 ,1/5,...`, האם קיימת סדרה חשבונית שמורכבת מאיברי הסדרה הנ"ל
-
באורך 5
-
בכל אורך
מקורות:נושאים:תורת המספרים -> חשבון השאריות -> סימני חלוקה הוכחה ודוגמה -> בניית דוגמה אלגברה -> סדרות -> סדרה חשבונית אריתמטיקה -> שברים תורת המספרים -> המחלק המשותף המקסימלי והכפולה המשותפת המינימלית -
-
50 בחזקת
הראו כי ב504 הספרות הימניות של `1+50+50^2+...+50^1000`
מופיעה כל ספרה בכמות שמתחלקת ב 12 פעמים
מקורות:נושאים:תורת המספרים -> חשבון השאריות -> סימני חלוקה -> סימני חלוקה ב-3 וב-9 אלגברה -> סדרות -> סדרה חשבונית אלגברה -> טכניקה אלגברית -> סכומים טלסקופיים -
שאלה
פי כמה סכום כל המספרים מ-1 עד 99 קטן מסכום כל המספרים מ-1 עד 9999?
מקורות:נושאים:אלגברה -> סדרות -> סדרה חשבונית -
נחלק ב-13
על דף נייר רושמים את כל המספרים הטבעיים בין 1 ל 2006, ומבצעים סדרת פעולות כמתואר להלן. בכל שלב מוחקים מספר כלשהו של מספרים מהרשימה ומסמנים את סכומם ב S. במקום המספרים שנמחקו מוסיפים מספר יחיד שהוא השארית המתקבלת מהחלוקה של S ב 13. לאחר מספר כלשהו של צעדים כאלו נותרו על הנייר שני מספרים בלבד. אחד מהם הוא 100. מצא את המספר השני.
מקורות:נושאים:תורת המספרים -> חשבון השאריות תורת המספרים -> חלוקה -> זוגיות אלגברה -> סדרות -> סדרה חשבונית- תחרות גרוסמן, 2006 שאלה 2
-
שיא המשחק הארוך
המשחק מתחיל עם שורה ובה 42 מטבעות, בכולם 'פלי' כלפי מעלה.
כל שחקן בתורו בוחר את אחד המטבעות בהם 'פלי' כלפי מעלה - הופך את המטבע שבחר, וגם את המטבע שצמוד לו מימין (אם קיים).
הצלחת להביא בתור שלך לכך שכל המטבעות מצביעים 'עץ'? ניצחת את המשחק!
לכל היותר, אחרי כמה תורות המשחק יסתיים?
מקורות:נושאים:אלגברה -> סדרות -> סדרה חשבונית -
סל תפוחי האדמה
לאיש היה סל ובו חמישים תפוחי אדמה. הוא הציע לבנו, כמעט שעשוע, שהוא יניח את תפוחי האדמה הללו על הקרקע בקו ישר. המרחק בין תפוח האדמה הראשון לשני יהיה יארד אחד, בין השני לשלישי שלושה יארדים, בין השלישי לרביעי חמישה יארדים, בין הרביעי לחמישי שבעה יארדים, וכן הלאה - עלייה של שני יארדים עבור כל תפוח אדמה עוקב שיונח. לאחר מכן הילד ירים אותם ויכניס אותם לסל אחד בכל פעם, כאשר הסל ממוקם ליד תפוח האדמה הראשון. כמה רחוק יצטרך הילד לנסוע כדי להשלים את המשימה של איסוף כולם? לא נתייחס למסע הכרוך בהנחת תפוחי האדמה, כך שהוא מתחיל מהסל כשהם כולם פרוסים. מקורות: -
שלושים ושלוש הפנינים
"אדם שאני מכיר," אמר טדי ניקולסון במסיבת משפחה מסוימת, "ברשותו מחרוזת של שלושים ושלוש פנינים. הפנינה האמצעית היא הגדולה והטובה מכולן, והשאר נבחרו וסודרו כך, שמתחילים מקצה אחד, כל פנינה עוקבת שווה £`100` יותר מקודמתה, ישר עד לפנינה הגדולה. מהקצה השני הפנינים עולות בערכן ב-£`150` עד לפנינה הגדולה. כל המחרוזת שווה £`65,000`. מה ערכה של הפנינה הגדולה הזו?"
"פנינים ופריטי לבוש אחרים," אמר הדוד וולטר, כשמחיר הפנינה היקרה התגלה, "מזכירים לי את אדם וחווה. הרשויות, ייתכן שאינכם יודעים, חלוקות לגבי מספר התפוחים שנאכלו על ידי אדם וחווה. יש הסבורים שחווה `8` (אכלה) ואדם `2` (גם), סך הכל `10` בלבד. אבל מתמטיקאים מסוימים חישבו זאת אחרת, וטוענים שחווה `8` ואדם סך הכל `16`. עם זאת, החוקרים האחרונים ביותר חושבים שהמספרים הנ"ל שגויים לחלוטין, כי אם חווה `8` ואדם `82`, הסך הכל חייב להיות `90`."
"טוב," אמר הארי, "נראה לי שאם היו ענקים בימים ההם, כנראה חווה `81` ואדם `82`, מה שייתן סך של `163`."
"אני לא מרוצה בכלל," אמרה מוד. "נראה לי שאם חווה `81` ואדם `812`, הם צרכו יחד `893`."
"אני בטוח שכולכם טועים," התעקש מר וילסון, "כי אני חושב שחווה `814` אדם, ואדם `8124` חווה, אז אנחנו מקבלים סך של `8,938`."
"אבל, תראו," התפרץ הרברט. "אם חווה `814` אדם ואדם `81242` מחייב את חווה, בטח הסך הכל היה `82,056`!"
בשלב זה הציע הדוד וולטר שהם יניחו לעניין. הוא הצהיר שזה בבירור מה שמתמטיקאים מכנים בעיה בלתי ניתנת להכרעה.
מקורות: -
בעיה בריבועים
יש ברשותנו שלושה לוחות מרובעים. שטח הפנים של הראשון מכיל חמישה רגל רבוע יותר מהשני, והשני מכיל חמישה רגל רבוע יותר מהשלישי. האם תוכלו לתת מידות מדויקות עבור צלעות הלוחות? אם תוכלו לפתור את החידה הקטנה הזו, נסו למצוא שלושה ריבועים בסדרה חשבונית, עם הפרש קבוע של `7` וגם של `13`. מקורות:- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 128