几何学, 平面几何学, 三角形
本主题探讨三角形(基本的三边多边形)的属性、类型(例如,等边、等腰、不等边、直角)和相关定理。问题通常涉及计算角度、边长、面积、周长以及应用三角形特定定理。
三角形全等 三角形相似-
问题
在边长为 1 的正方形 ABCD 内标记一点 E,在正方形外标记一点 F,使得三角形 ABE 和 DAF 均为等边三角形。计算五边形 CBEFD 的面积。
来源:

-
问题
在图中绘制了一个梯形,在其每个底边上选择了 5 个点。这些点的一部分通过直线段连接。证明蓝色区域的面积之和等于橙色区域的面积之和。
来源:
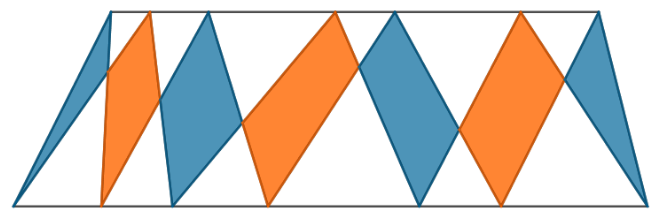
-
问题
将一个正方形切成三块,然后用它们组成一个各边都不相等的锐角三角形。
-
问题
两个全等的三角形形成一个如图像所示的六芒星。证明阴影区域的面积等于条纹区域的面积。
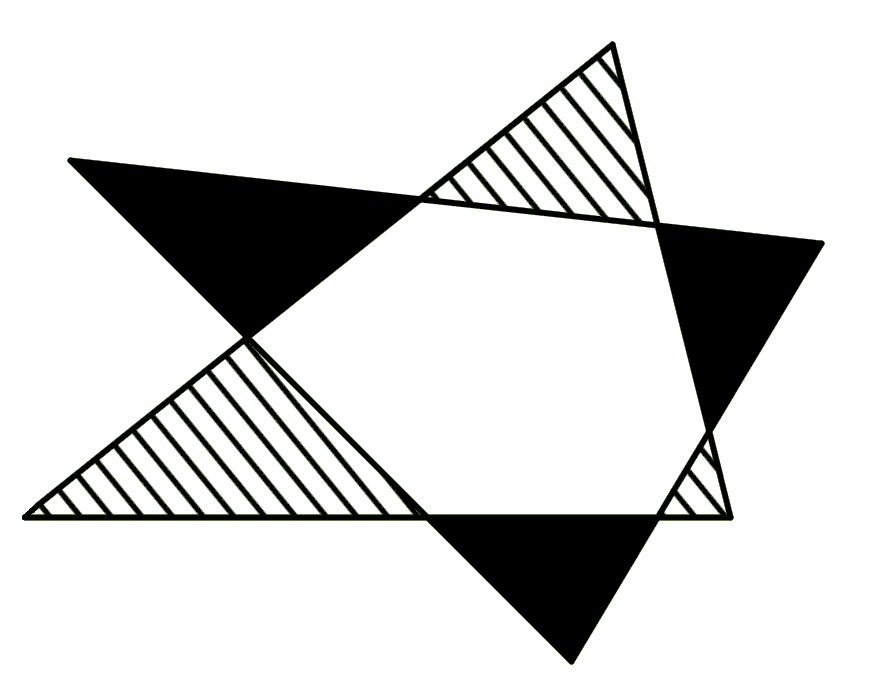
-
五边形
在凸五边形 `ABCDE` 中,已知: `AE=AD`, `AB=AC` 且 `angle CAD=angle ABE + angle AEB`。
在三角形 `ABE` 中,作中线 `AM`。 证明: `AM` 的长度是线段 `CD` 长度的一半。
来源: -
问题
给定一个具有 n 个顶点的正多边形。计算顶点与多边形顶点重合的不同三角形(非全等三角形)的数量
来源: -
点在哪里?
在凸六边形 ABCDEF 中,三角形
ACE 和 BDF 是等边且全等的。证明
连接六边形对边中点的三条线段
交于一点。来源: -
在线条上的三角形
六个全等的等腰三角形如图所示放置在一起。
证明点 C、F 和 M 在一条直线上。 来源:
来源: -
问题
给定一个圆锥(其对称轴位于中心,垂直于其底面),其高度为 6,底面是一个半径为 `sqrt2` 的圆。圆锥内接一个立方体——它位于圆锥的底面上,并且其所有上顶点都接触圆锥。求立方体的边长。解释你的答案。
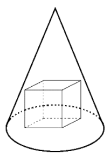 来源:
来源: -
问题
对于任意三角形,作内切圆的切线,使其平行于三角形的边。 这些切线从原始三角形切割出三个小三角形。 证明这三个小三角形的内切圆半径之和等于原始三角形的内切圆半径。