代数学
代数学是数学的一个广泛分支,使用符号(通常是字母)来表示数字并陈述规则和关系。它涉及操作表达式,解方程和不等式,以及研究函数和结构。问题涵盖这些主题的广泛范围。
代数技巧 方程 不等式 应用题 数列-
问题
证明以下等式:
`1+3+5+...+(2n-1)=n^2`
-
樱桃和蓝莓
`175` 公斤樱桃比 `125` 公斤蓝莓贵,但比 `126` 公斤蓝莓便宜。此外,已知每公斤樱桃的价格是整数,每公斤蓝莓的价格也是整数。
证明 `80` 元不足以购买一公斤蓝莓和三公斤樱桃。
С.Фумин
来源: -
框架
在一个给定的方格纸上有一个大小为 `NxxN` 的正方形。我们考虑其厚度为一个方格的框架。它由 `4*(N-1)` 个方格组成。
你是否能将 `4*(N-1)` 个连续整数(不一定是正数)填入框架的方格中,使得满足以下条件:
对于每个顶点都在框架上且边与原始正方形的对角线平行的矩形,其顶点上的数字之和等于一个常数。 这也包括“退化”的宽度为零的矩形,这些矩形与正方形的对角线重合 - 在这种情况下,只需将正方形的相对顶点的两个数字相加
对于:
a. `N=3`
b. `N=4`
c. `N=5`
来源: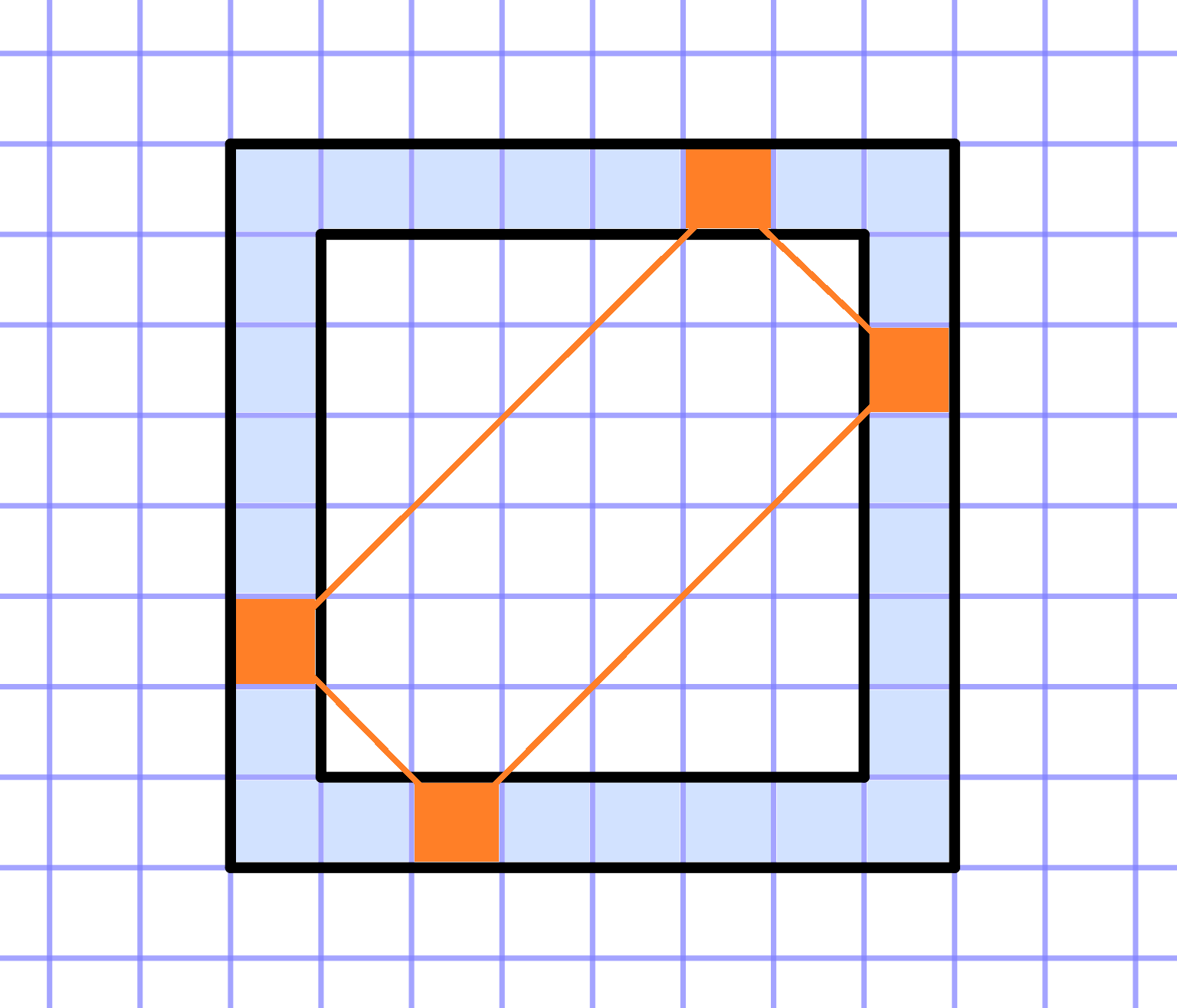
-
数字的乘积
对于自然数 `x`,记 `P(x)` 为 `x` 的各位数字的乘积,记 `S(x)` 为 `x` 的各位数字之和。
方程有多少个解:
`P(P(x))+P(S(x))+S(P(x))+S(S(x))=1984`
来源: -
问题
请在不使用计算器的情况下找出以下表达式的值:
`(sqrt(sqrt(2)-1))/(sqrt(sqrt(2)+1))+ (sqrt(sqrt(3)-sqrt(2)))/(sqrt(sqrt(3)+sqrt(2)))+ (sqrt(2-sqrt(3)))/(sqrt(2+sqrt(3)))`
-
问题
`120` 个相同的球被排列成一个三角形金字塔。金字塔有多少层?
注意:这是一个金字塔,即三维形状,而不是平面上的三角形。
-
问题
房间里有`3`条腿的圆形椅子和`4`条腿的方形椅子,总共有`8`把椅子。 如果房间里总共有`27`条腿,那么其中有多少是方形椅子?
-
问题
在 Ella 的房子里有三个入口和 `13` 层楼(从 `0` 到 `12`,公寓位于除底层外的所有楼层)。每个入口,每层楼有五间公寓。Ella 住在 `73` 号公寓。她住在哪个入口,哪层楼?
-
问题
Avi 邀请了客人。他们知道他住在 `333` 号公寓,在 `10` 号楼,但他们不知道是哪一层。楼里有 `9` 层楼,并且已知每层楼的公寓数量相等。客人们想使用电梯。他们可以提前计算出需要在电梯里按哪一层吗?
-
问题
七只狼在七天内吃掉七只羊。那么,`9` 只狼吃掉 `9` 只羊需要多长时间?