组合数学
组合数学是计数的艺术。它处理对象的选择、排列和组合。问题涉及确定执行任务、排列项目(排列)或选择子集(组合)的方式数量,通常使用乘法原理和加法原理等原则。
鸽巢原理 双重计数 二项式系数和帕斯卡三角形 乘法法则/乘积法则 图论 匹配 归纳法(数学归纳法) 博弈论 组合几何学 不变量 案例分析/检查案例 过程/程序 数字表格 着色问题-
问题
将给定的形状切割成八个全等的部分:

-
问题
将给定的形状切割成16个全等的部分:
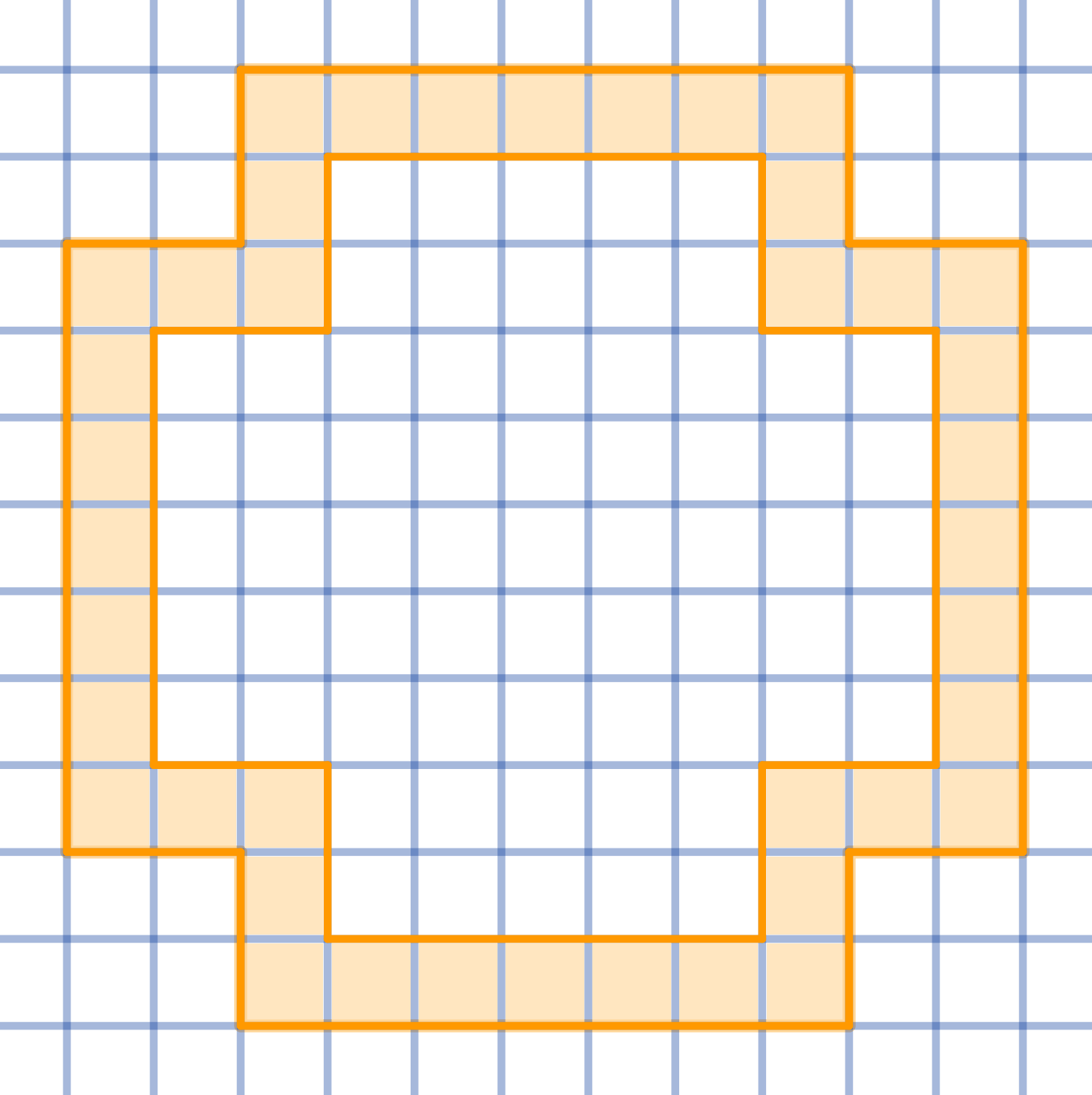
-
木棍上的蚂蚁
在一根长一米的木棍上有 `10` 只蚂蚁,每边 `5` 只,相距一厘米(见图)。木棍左侧的蚂蚁向右走,木棍右侧的蚂蚁向左走。每只蚂蚁的速度恒定,为每秒一厘米。当两只蚂蚁相遇时,它们都会改变方向并开始彼此远离。当任何一只蚂蚁到达木棍的末端时,它就会掉落(蚂蚁是非常愚蠢的生物)。

A. 是否会出现所有蚂蚁都从木棍上掉下来的情况,如果可以,那么需要多长时间?
B. 蚂蚁之间会发生多少次碰撞?
-
牛奶和咖啡
一. 汉娜有两个杯子,一个装牛奶,另一个装咖啡。牛奶和咖啡的量相同。汉娜将两茶匙牛奶倒入咖啡杯中,搅拌均匀,然后将两茶匙咖啡从咖啡杯中倒入牛奶杯中。现在她有两个杯子,每个杯子都装有咖啡和牛奶的混合物。哪个更多 – 咖啡杯中的牛奶还是牛奶杯中的咖啡?
二. 同样的问题,但这次汉娜将牛奶加入咖啡中不搅拌。
-
圆圈
六年级有 `70` 个学生。其中 `27` 人参加戏剧社,`32` 人在合唱团唱歌,`22` 人练习柔道。戏剧社有 `10` 个合唱团成员,合唱团有 `6` 个柔道成员,柔道社有 `8` 个也参加戏剧社的成员。有三个孩子同时参加戏剧社、柔道社和合唱团。那么有多少六年级的学生没有参加这三个社团中的任何一个?
-
圆桌骑士
圆桌旁坐着 12 位骑士,他们每个人要么是精灵,要么是矮人。已知精灵的数量多于矮人的数量。证明存在两个面对面坐着的精灵。
如果骑士的总数为 120,这个结论仍然成立吗?
-
问题
证明:从五个整数中,可以选择两个,它们的差能被`4`整除。
-
问题
A. 证明在 `11` 个自然数中,总能选出两个数,它们的个位数相同。
B. 证明在 `11` 个自然数中,总能选出两个数,它们的差能被 `10` 整除。
-
问题
有`21`个孩子,他们总共有`200`个坚果。证明存在两个孩子,他们拥有相同数量的坚果。
-
问题
在一个班级里有 `30` 名学生。在一次考试中,彭哈斯犯了 `13` 个错误,其余的人犯的错误都更少。证明有三名学生犯了相同数量的错误。