数论
数论是数学的一个分支,关注整数的性质。主题包括素数、可除性、同余(模算术)、丢番图方程和整数函数。问题通常需要对数字进行分析性和创造性思考。
素数 中国剩余定理 模算术/余数算术 最大公约数(GCD)和最小公倍数(LCM) 三角形数 除法-
问题
一个国际象棋的马从 `a1` 格出发,经过若干步后回到了同一格。
马有可能走了奇数步吗?
-
问题
一个骑士从 `a1` 格出发,到达 `h8` 格。是否可能它在途中恰好访问了棋盘上的每个格子一次?
-
问题
曾经生活在地球上的每个人都进行了特定次数的握手(包括 0 次)。 证明进行了奇数次握手的人数是偶数。
-
问题
这个神奇的国度由`25`个地区组成。是否有可能每个地区都与奇数个其他地区相邻?
-
问题
给定七个整数 `a_1,a_2,a_3,...,a_7`, 设 `b_1,b_2,b_3,...,b_7` 是以不同顺序排列的相同数字。证明数字 `(a_1-b_1)(a_2-b_2)*...*(a_7-b_7)` 必然是偶数。
-
问题
从棋盘上切掉两个对角(例如,`a1` 和 `h8`)。 你能用多米诺骨牌铺满剩下的棋盘吗?
-
问题
证明两个连续整数的乘积总是偶数。
-
问题
黑板上写着数字:`1, 2, 3, …, 2016, 2017`。每次操作可以选择黑板上的两个数字,将它们擦除,然后写上它们的(正)差。经过多次这样的操作后,黑板上只剩下一个数字。这可能为零吗?
-
框架
在一个给定的方格纸上有一个大小为 `NxxN` 的正方形。我们考虑其厚度为一个方格的框架。它由 `4*(N-1)` 个方格组成。
你是否能将 `4*(N-1)` 个连续整数(不一定是正数)填入框架的方格中,使得满足以下条件:
对于每个顶点都在框架上且边与原始正方形的对角线平行的矩形,其顶点上的数字之和等于一个常数。 这也包括“退化”的宽度为零的矩形,这些矩形与正方形的对角线重合 - 在这种情况下,只需将正方形的相对顶点的两个数字相加
对于:
a. `N=3`
b. `N=4`
c. `N=5`
来源: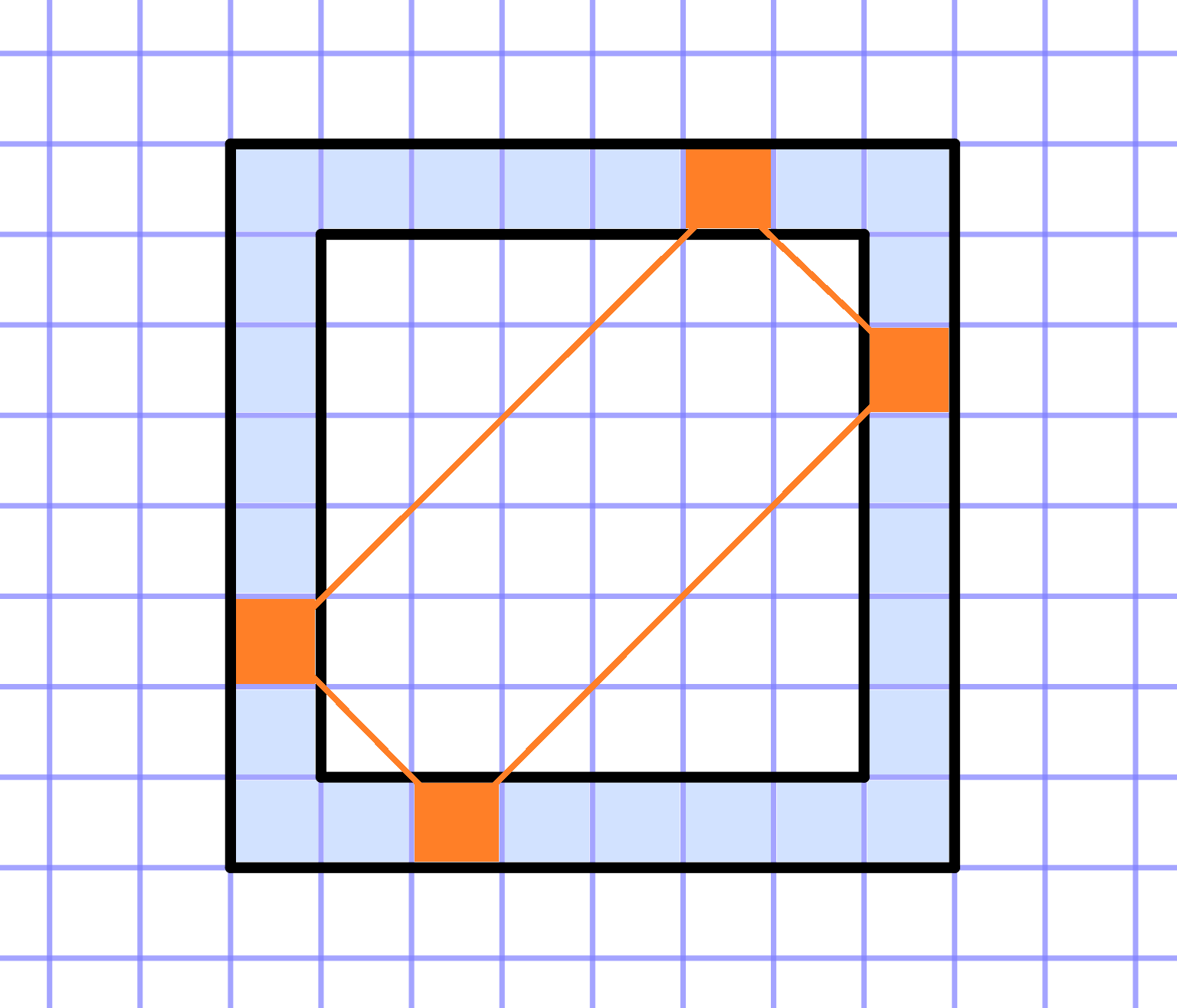
-
问题
证明不能将给定的形状切割成多米诺骨牌:
