几何学, 平面几何学
平面几何学关注平面二维表面上的图形和形状。它涵盖点、线、角、多边形(如三角形和四边形)和圆的属性。问题通常涉及与这些元素相关的证明、作图和计算。
面积计算 三角形 圆 对称性 角度计算 勾股定理 三角形不等式-
阴阳四分之一
图中形状的构造方式如下:将半圆的直径分成两个相等的部分,并以它们为直径构建另外两个半圆:一个在内部,另一个在外部。
将该形状分成两个全等的部分。
-
问题
在一个四边形中,所有对角线和所有边的长度都小于 1。证明可以用半径为 0.9 的圆覆盖该四边形。
来源: -
正多边形和圆
A.
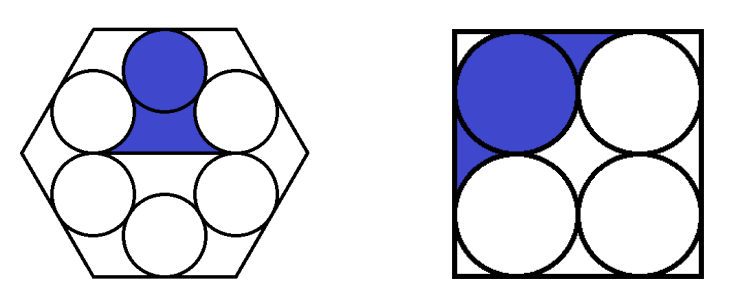
在右边的图中,有一个正方形,里面有4个圆。这些圆的半径相等,每个圆与另外两个圆相切,并且与正方形的两条边相切。求正方形中蓝色部分面积与白色部分面积的比率。
B.
在左边的图中,有一个六边形,里面有6个半径相同的圆。每个圆与另外两个圆相切,并且与六边形的一条边在中间位置相切。求六边形中蓝色部分面积与白色部分面积的比率。
(答案格式:"x, y" 例如 "1/8, 7/100")
来源: -
图形面积
图中,半圆的面积等于 1。求大图形的面积,已知图中所有弯曲的线段都是四分之一圆弧。
来源: -
圆的切线
已知两个三角形 ACE, BDF
相交于 6 个点: G,H,I,J,K,L
如图所示。已知每个四边形
EFGI ,DELH ,CDKG ,BCJL ,ABIK 都有一个内切圆。
FAHJ 四边形是否也可能有一个内切圆?
 来源:
来源: -
平面上的集合
A. 是否存在一个平面上的集合 A,使得它与每个圆的交集恰好包含两个点?
B. 是否存在一个平面上的集合 B,使得它与每个半径为 1 的圆的交集恰好包含两个点?
来源: -
轮子转向他
图中所有 6 个齿轮都在无滑动的情况下相互接触旋转。左侧齿轮的直径为 15.7 厘米,它每分钟旋转 12 圈。
已知小齿轮每秒旋转一圈。
小齿轮的直径是多少?
来源: -
问题
给定一条直线 `l` 和两个点 `A,B`,它们与该直线的距离不同。在直线上找到点 `C`,使得线段 `AC` 和 `AB` 的长度之差最大。
来源: -
问题
设 M 为平面上点的集合。如果可以从 M 中移除一个点,使得 O 是剩余点的通常对称中心,则称 O 为部分对称中心。一个平面上的有限点集可以有多少个部分对称中心?
来源:
В. Прасолов -
纸张堆叠
桌子上有一些相同的矩形纸张。已知最上面的纸张覆盖了任何其他纸张超过一半的面积。是否一定可以在桌子上钉一个钉子,使其穿过所有这些纸张?


