几何学, 平面几何学
平面几何学关注平面二维表面上的图形和形状。它涵盖点、线、角、多边形(如三角形和四边形)和圆的属性。问题通常涉及与这些元素相关的证明、作图和计算。
面积计算 三角形 圆 对称性 角度计算 勾股定理 三角形不等式-
问题
将给定的形状切割成四个全等的部分:
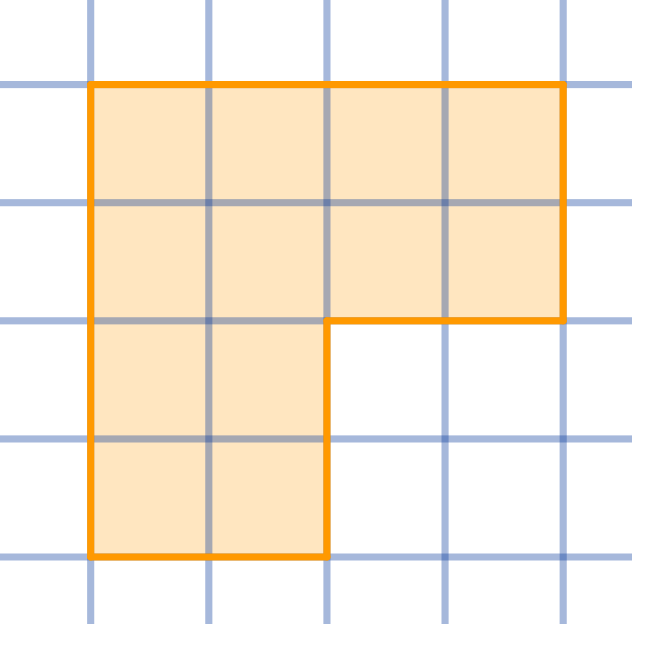
-
问题
已知给定形状的所有角都是直角。将形状切割成两个面积相等的多边形。 只允许使用没有刻度的直尺。
-
灰色区域
在图中,一个矩形由 5 个大小为 `2 times 2 ` 的正方形组成,并有一条对角线穿过它。
求阴影区域的面积。
来源: -
问题
在一个正五边形的顶点上写着数字 `1,2,3,4,5`,每个顶点恰好写一个数字。如果一个顶点三元组构成一个等腰三角形,且其顶点的数字大于另两个顶点或小于另两个顶点,则该三元组被称为成功的。
求出可能的最大成功三元组数量。
-
分割成四个相等的部分
如果几何形状在彼此叠放时重合,则称它们全等。将下面的形状切割成四个全等的部分:
来源: -
将船切成两半
如果将几何形状放置在彼此之上时可以完全重合,则称它们是全等的。将形状切割成两个全等的部分
来源: -
点在哪里?
在凸六边形 ABCDEF 中,三角形
ACE 和 BDF 是等边且全等的。证明
连接六边形对边中点的三条线段
交于一点。来源: -
问题
给定一个圆锥(其对称轴位于中心,垂直于其底面),其高度为 6,底面是一个半径为 `sqrt2` 的圆。圆锥内接一个立方体——它位于圆锥的底面上,并且其所有上顶点都接触圆锥。求立方体的边长。解释你的答案。
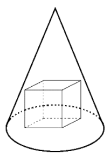 来源:
来源: -
问题
Shlomi 有一个尺寸为 `5xx5` 厘米的扁平盒子。 Shlomi 声称,任何可以放入此盒子的矩形,其所有边都必须小于 5 厘米。 他是对的吗?
-
问题
在空间中给定 30 个非退化的向量。证明至少存在 2 个向量,它们之间的夹角不大于 45 度。
来源:
一. 托尔皮戈



