证明与示例
此类别强调构建严谨论证(证明)以建立普遍真理,以及使用具体实例(示例)来说明概念、检验猜想或寻找反例的核心数学活动。问题可能要求其中之一或两者兼有。
构造示例/反例 反证法-
问题
游戏在一个无限的平面上进行。一个玩家移动狼,另一个玩家移动 K 只羊。狼走一步后,一只羊走一步,然后狼再走,以此类推。每一步,狼或羊最多只能向任何方向移动一米。在任何初始状态下,狼是否总能抓住至少一只羊?
来源: -
问题
一只蚱蜢可以向前跳 `80` 厘米,也可以向后跳 `50` 厘米。蚱蜢是否可以在少于 `7` 跳之内,恰好从起点移动一米 `70` 厘米?
-
问题
是否可以将一个三角形切割成以下四个凸形状:三角形、四边形、五边形和六边形?
-
问题
给定一个 `10×10` 厘米的纸。你能否从这张纸上剪出若干个圆,使得它们的直径之和大于 `5` 米?
-
问题
一个平面被涂成两种颜色(也就是说,平面上的每个点都被涂成这两种颜色之一)。证明存在平面上距离为 `1` 的两个点,且它们具有相同的颜色。
-
问题
是否存在一个四边形,可以通过两条直线切割成 `6` 个部分?请给出理由或提供一个例子。
-
9公斤的米
你有`9` 公斤的米。 如何用一个天平和两个砝码(`200`克和`50`克)称出`2`公斤的米,并且只能称三次?
-
框架
在一个给定的方格纸上有一个大小为 `NxxN` 的正方形。我们考虑其厚度为一个方格的框架。它由 `4*(N-1)` 个方格组成。
你是否能将 `4*(N-1)` 个连续整数(不一定是正数)填入框架的方格中,使得满足以下条件:
对于每个顶点都在框架上且边与原始正方形的对角线平行的矩形,其顶点上的数字之和等于一个常数。 这也包括“退化”的宽度为零的矩形,这些矩形与正方形的对角线重合 - 在这种情况下,只需将正方形的相对顶点的两个数字相加
对于:
a. `N=3`
b. `N=4`
c. `N=5`
来源: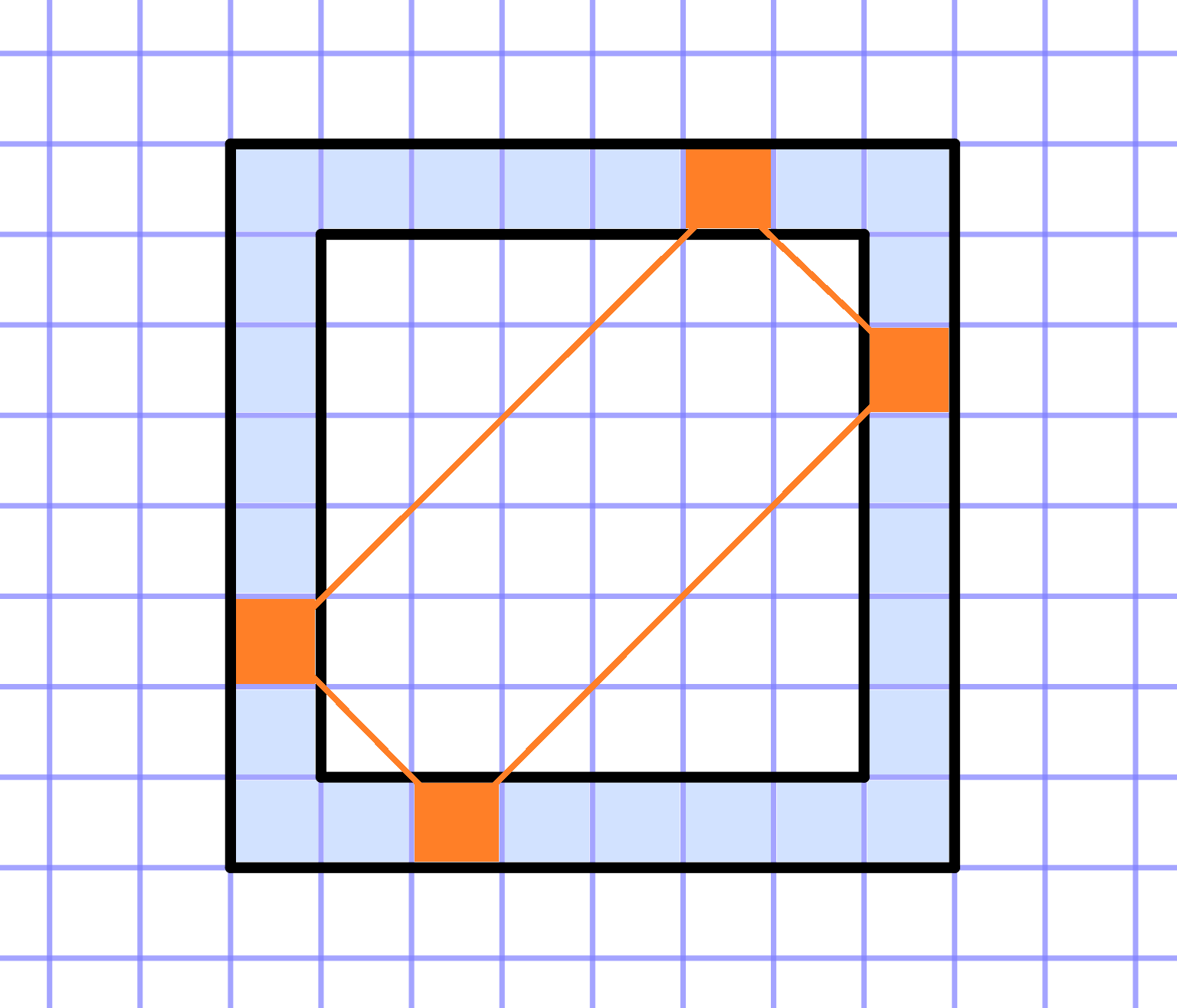
-
问题
一. 假设您有一个12升的大油罐,以及两个空的容器,分别为5升和8升。您是否能够将油分成两个相等的部分?您只有这些容器,没有其他测量工具。
二. 同样的问题,但不是5升的容器,而是一个4升的容器。
-
问题
`120` 个相同的球被排列成一个三角形金字塔。金字塔有多少层?
注意:这是一个金字塔,即三维形状,而不是平面上的三角形。