几何学
几何学是数学的一个分支,关注点、线、面、体以及更高维度类似物的属性和关系。预期问题涉及计算各种形状的长度、角度、面积和体积,理解几何定理,以及解决与空间推理相关的问题。
立体几何/空间几何 三角学 球面几何学 平面几何学 向量-
平面上的集合
A. 是否存在一个平面上的集合 A,使得它与每个圆的交集恰好包含两个点?
B. 是否存在一个平面上的集合 B,使得它与每个半径为 1 的圆的交集恰好包含两个点?
来源: -
六边形平铺
给出两种类型的瓷砖。第一种类型的每个瓷砖的形状是边长为 1 的正六边形。第二种类型的每个瓷砖的形状是边长为 2 的正六边形。假设每种类型的瓷砖都有无限的供应。是否可以用这些瓷砖平铺整个平面,同时使用两种类型的瓷砖?
来源: -
三角形的边长
设 `n > 2` 为整数,且 ` t_1,t_2,...,t_n` 为正实数,满足
`(t_1+t_2+...+t_n)(1/t_1 + 1/t_2 + ... + 1/t_n) < n^2+1`
证明对于所有 i,j,k 满足 `1<=i<j<k<=n`,数集 `t_i,t_j,t_k` 均为某个三角形的边长。
来源: -
平面上的旅行
给定一个平面直角坐标系 x-y。需要从点 (1,0) 到达点 (2006,2005),每次移动可以向上(沿 y 轴正方向)移动一个单位,或者向右(沿 x 轴正方向)移动一个单位。
a. 有多少种不同的路径可以完成这个任务?
b. 如果不允许在任何阶段通过位于直线 x=y 上的点,那么有多少种不同的路径可以完成这个任务?
来源: -
轮子转向他
图中所有 6 个齿轮都在无滑动的情况下相互接触旋转。左侧齿轮的直径为 15.7 厘米,它每分钟旋转 12 圈。
已知小齿轮每秒旋转一圈。
小齿轮的直径是多少?
来源: -
三角形公园的小路
在一个公园里,有3条直线小路构成一个三角形(没有其他小路)。公园的入口位于每条小路的中间,并且在三角形的每个顶点都悬挂着一盏灯。从每个入口处测量沿公园小路到对面顶点的灯的最短步行距离。结果发现,3个距离中有2个彼此相等。三角形一定是等腰三角形吗?
来源:
-
问题
在边长为 1 的正方形 ABCD 内标记一点 E,在正方形外标记一点 F,使得三角形 ABE 和 DAF 均为等边三角形。计算五边形 CBEFD 的面积。
来源:

-
问题
将图中的形状分成7个全等的部分。
来源:
-
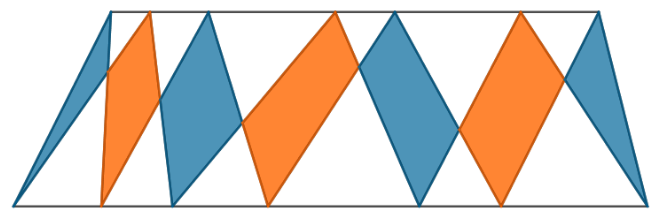
问题
在图中绘制了一个梯形,在其每个底边上选择了 5 个点。这些点的一部分通过直线段连接。证明蓝色区域的面积之和等于橙色区域的面积之和。
来源: